1. 2차원 배열 다루기
1) 2차원 배열 응용
문제 1) 교점에 별 만들기
코딩테스트 연습 - 교점에 별 만들기 | 프로그래머스 스쿨
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
● 문제 풀이
문제 풀이 흐름
1. 모든 직선 쌍에 대해 반복
A. 교점 좌표 구하기
B. 정수 좌표만 저장
2. 저장된 정수들에 대해 x,y 좌표의 최댓값, 최솟값 구하기
3. 구한 최댓값, 최솟값을 이용하여 2차원 배열의 크기 결정
4. 2차원 배열에 별 표시
5. 문자열 배열로 변환 후 반환
코드 작성
- 좌표를 나타내는 클래스
- 데이터를 나타내는 클래스이므로 final 키워드를 사용하여 불변성을 갖게 하고, 생성자로 초기화
- 문제에서 좌표 범위를 주어지지 않았기 때문에 x,y는 long으로 표현
private static class Point {
public final long x,y;
private Point(long x, long y) {
this.x = x;
this.y = y;
}
}
1. 모든 직선 쌍에 대해 반복
- 이중 반복문으로 간단히 구현
for(int i=0; i<line.length; i++) {
for(int j=i+1; j<line.length; j++) {
//line[i], line[j]를 이용하여 1-A, 1-B 수행
}
}
1-A. 교점 좌표 구하기
- 별도의 메서드로 분리하여 구현
- 두 직선의 정보를 매개변수로 받아, 그 교점이 정수이면 Point 객체를 반환하는 메서드를 선언
private Point intersection(long a1, long b1, long c1, long a2, long b2, long c2) {
//교점 구해서 반환하기
return null;
}

- 위 공식을 이용하여 교점을 구하고, 정수일 때만 반환하도록 메서드 구현
double x = (double)(b1*c2-b2*c1) / (a1*b2-a2*b2);
double y = (double)(a2*c1-a1*c2) / (a1*b2-a2*b1);
if(x%1!=0 || y%1!=0) return null;
return new Point((long)x, (long)y);
1-B 정수 좌표만 저장
- 좌표를 저장할 리스트를 만들고, 객체가 반환되었을 때만 리스트에 저장
List<Point> points = new ArrayList<>();
for(int i=0; i<line.length; i++) {
for(int j=i+1; j<line.length; j++) {
Point intersection = intersection(line[i][0],line[i][1],line[i][2],
line[j][0],line[j][1],line[j][2]);
if(intersection!=null) {
points.add(intersection);
}
}
}
2. 저장된 정수들에 대해 x,y 좌표의 최댓값, 최솟값 구하기
- 별을 표시할 2차원 배열은 정확히 별을 표시할 수 있을 정도로 작게 잡아야 한다.
- 이를 위해 각 좌표의 최댓값과 최솟값을 구해야 한다.
- 가장 작은 x,y 좌표를 포함하는 Point 객체와 가장 큰 x,y 좌표를 갖는 Point 객체를 반환하는 두 함수 선언
private Point getMinimumPoint(List<Point>points) {
//가장 작은 좌표 찾기
return null;
}
private Point getMaximumPoint(List<Point>points) {
//가장 큰 좌표 찾기
return null;
}
getMinimumPoint() 메서드
private Point getMinimumPoint(List<Point> points) {
long x = Long.MAX_VALUE:
long y = Long.MIN_VALUE:
for(Point p : points) {
if(p.x <x) x=p.x;
if(p.y <y) y=p.y;
}
return new Point(x,y);
}
getMaximumPoint() 메서드
private Point getMaximumPoint(List<Point> points) {
long x = Long.MIN_VALUE;
long y = Long.MAX_VALUE;
for(Point p : points) {
if(p.x > x) x=p.x;
if(p.y > y) y=p.y;
}
return new Point(x,y);
}
3. 구한 최댓값, 최솟값을 이용하여 2차원 배열의 크기 결정
- 위 두 메서드를 사용해서 2차원 배열 크기 알기
Point minimum = getMinimumPoint(points);
Point maximum = getMaximumPoint(points);
int width = (int)(maximum.x - minimum.x+1);
int height = (int)(maximum.y - minimum.y+1);
- 이 값을 사용하여 2차원 배열을 선언하고 초기화
- 문자를 이용하여 각 좌표를 표시하기 때문에 char 자료형의 2차원 배열로 선언
char[][] arr = new char[height][width];
for(char[] row : arr) {
Arrays.fill(row,'.');
}
4. 2차원 배열에 별 표시
- 별을 찍을 위치인 교점 정보는 points 변수에 있으므로 이를 순회하면서 별을 찍어주면 된다.
for(Point p : points) {
//2차원 배열에 별 찍기
}
- 2차원 배열에서 (0,0)은 실제 교점의 (0,0)이 아니다. 교점을 표현할 수 있는 가장 작은 크기로 2차원 배열을 선언했기 때문에 별을 제대로 표시하려면 좌표를 변환시켜 주어야 함
- 2차원 배열의 좌표는 일반 좌표와 비교했을 때 y축 방향이 반대고, minimum과 maximum으로 그 크기가 결정됨
int x = (int)(p.x-minimum.x);
int y = (int)(maximum.y - p.y);
arr[y][x] = '*';
전체 코드
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Solution {
//좌표를 나타내는 클래스
private static class Point {
public final long x, y;
private Point(long x, long y) {
this.x = x;
this.y = y;
}
}
//교점을 구하고, 정수일 때만 반환
private Point intersection(long a1, long b1, long c1, long a2, long b2, long c2) {
double x = (double) (b1 * c2 - b2 * c1) / (a1 * b2 - a2 * b1);
double y = (double) (a2 * c1 - a1 * c2) / (a1 * b2 - a2 * b1);
if (x % 1 != 0 || y % 1 != 0) return null;
return new Point((long) x, (long) y);
}
//최솟값 구하기
private Point getMinimumPoint(List<Point> points) {
long x = Long.MAX_VALUE;
long y = Long.MAX_VALUE;
for (Point p : points) {
if (p.x < x) x = p.x;
if (p.y < y) y = p.y;
}
return new Point(x, y);
}
//최댓값 구하기
private Point getMaximumPoint(List<Point> points) {
long x = Long.MIN_VALUE;
long y = Long.MIN_VALUE;
for (Point p : points) {
if (p.x > x) x = p.x;
if (p.y > y) y = p.y;
}
return new Point(x, y);
}
public String[] solution(int[][] line) {
List<Point> points = new ArrayList<>();
//정수 좌표만 저장
for (int i = 0; i < line.length; i++) {
for (int j = i + 1; j < line.length; j++) {
Point intersection = intersection(line[i][0], line[i][1], line[i][2], line[j][0], line[j][1], line[j][2]);
if (intersection != null) {
points.add(intersection);
}
}
}
Point minimum = getMinimumPoint(points);
Point maximum = getMaximumPoint(points);
//2차원 배열 크기 구하기
int width = (int) (maximum.x - minimum.x + 1);
int height = (int) (maximum.y - minimum.y + 1);
char[][] arr = new char[height][width];
for (char[] row : arr) {
Arrays.fill(row, '.');
}
//2차원 배열에 별 표시
for (Point p : points) {
int x = (int) (p.x - minimum.x);
int y = (int) (maximum.y - p.y);
arr[y][x] = '*';
}
//문자열 배열로 변환 후 반환
String[] result = new String[arr.length];
for (int i = 0; i < result.length; i++) {
result[i] = new String(arr[i]);
}
return result;
}
}
문제 2) 삼각 달팽이
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
● 문제 풀이
2차원 배열로 표현된 삼각형
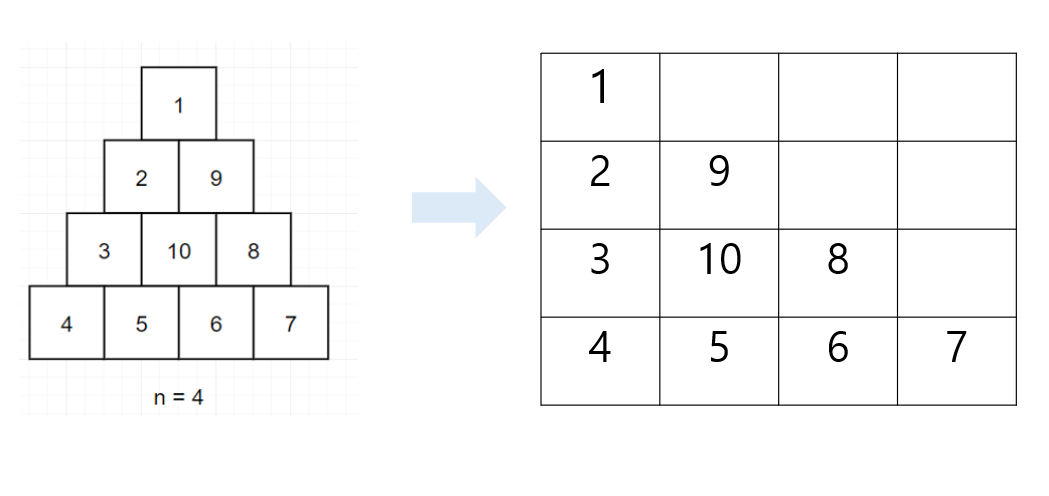
- 문제 조건인 반시계 방향으로 '달팽이 채우기'를 진행하는 것은 2차원 배열에서 반시계 방향인 아래->오른쪽->왼쪽 위로 진행하는 것
문제 풀이 흐름
1. n*n 2차원 배열 선언
2. 숫자를 채울 현재 위치를 (0,0)으로 설정
3. 방향에 따라 이동할 수 없을 때까지 반복하면서 숫자 채우기
A. 아래로 이동하면서 숫자 채우기
B. 오른쪽으로 이동하면서 숫자 채우기
C. 왼쪽 위로 이동하면서 숫자 채우기
4. 채워진 숫자를 차례대로 1차원 배열에 옮겨서 반환
코드 작성
1. n*n 2차원 배열 선언
- 가장 먼저 삼각형을 표현할 2차원 배여로가 채워 넣을 숫자를 선언
- triangle 변수는 2차원 배열로 가로 n, 세로 n의 삼각형을 표현하기 위해 n*n 2차원 배열로 선언
- v 변수는 채워 넣을 숫자로, 숫자를 triangle에 기록할 때마다 1씩 증가
int[][] triangle = new int[n][n];
int v = 1;
2. 숫자를 채운 현재 위치를 (0,0)으로 설정
- 이 배열에 숫자를 넣을 위치를 변수로 선언하고 (0,0)으로 초기화
- x,y는 위치 변수로 숫자를 기록할 때마다 아래,오른쪽,왼쪽 위 중 하나의 방향으로 이동
int x = 0;
int y = 0;
3. 방향에 따라 이동할 수 없을 때까지 반복하면서 숫자 채우기
- 아래,오른쪽, 왼쪽 위로 이동하면서 숫자를 계속해서 채워 넣어야 하기 때문에 무한 루프로 작성
while(true) {
//아래로 이동
//오른쪽으로 이동
//왼쪽 위로 이동
}
3-A. 아래로 이동하면서 숫자 채우기
- 아래로 이동하는 것은 y값이 증가하는 것
while(true) {
triangle[y][x] = v++;
if(y+1 == n || triangle[y+1][x]!=0) break;
y+=1;
}
- 이 반복문에서 빠져나왔다는 것은 더 이상 아래로 진행할 수 없다는 의미
- 아래로 진행할 수 없다면 오른쪽으로 진행해야 하지만, 오른쪽으로도 진행할 수 없는 경우가 있다. 아래로 진행하는 것이 삼각형을 채우는 마지막 진행 방향이면 여기에서 숫자를 채우는 것을 멈춰야 한다.
- 오른쪽으로 이동할 수 없는 경우에는 반복문을 탈출하도록 작성해서 오른쪽으로 이동할 수 있을 때만 진행
//아래로 이동
while(true) {
triangle[y][x] = v++;
if(y+1 == n || triangle[y+1][x]!=0) break;
y+=1;
}
if(x+1 == n || triangle[y][x+1] !=0) break;
3-B. 오른쪽으로 이동하면서 숫자 채우기
- 오른쪽으로 이동하는 것은 x값이 증가하는 것
//오른쪽으로 이동
while(true) {
triangle[y][x] = v++;
if(x+1 == n || triangle[y][x+1] !=0) break;
x+=1;
}
if(trianlge[y-1][x-1]!=0) break;
x-=1;
y-=1;
3-C. 왼쪽 위로 이동하면서 숫자 채우기
- 왼쪽 위로 이동하는 것은 x값과 y값이 감소하는 것
//왼쪽 위로 이동
while(true) {
triangle[y][x] = v++;
if(triangle[y-1][x-1]!=0) break;
x-=1;
y-=1;
}
if(y+1==n || triangle[y+1][x] !=0) break;
y+=1;
4. 채워진 숫자를 차례대로 1차원 배열에 옮겨서 반환
- triangle에 채운 숫자들을 1차원 배열로 구성하여 반환
- v 변수에는 채워 넣은 마지막 숫자 +1이 들어 있으므로 v-1이 채워 넣은 숫자 개수가 된다. 따라서 1차원 배열은 v-1의 크기로 선언
int[] result = new int[v-1];
- 2차원 배열에서는 삼각형이 왼쪽으로 몰려 있는 직각 삼각형으로 들어 있다는 것을 이용하면 다음과 같이 이중 반복문으로 1차원 배열에 숫자를 넣어 줄 수 있다.
int index = 0;
for(int i=0; i<n; i++) {
for(int j=0; j<=i; j++) {
result[index++] = triangle[i][j];
}
}
전체 코드
class Solution {
public int[] solution(int n) {
int triangle[][] = new int[n][n];
int v = 1;
int x = 0;
int y = 0;
while(true){
//아래로 이동
while(true) {
triangle[y][x] = v++;
if(y+1 == n || triangle[y+1][x] !=0) break;
y+=1;
}
if(x+1 == n || triangle[y][x+1] !=0) break;
x+=1;
//오른쪽으로 이동
while(true) {
triangle[y][x] = v++;
if(x+1 == n || triangle[y][x+1] !=0) break;
x+=1;
}
if(triangle[y-1][x-1] != 0) break;
x -= 1;
y -=1;
//왼쪽 위로 이동
while(true) {
triangle[y][x] = v++;
if(triangle[y-1][x-1]!=0) break;
x-=1;
y-=1;
}
if(y+1==n || triangle[y+1][x] !=0) break;
y+=1;
}
int result[] = new int[v-1];
int index = 0;
for(int i=0; i<n; i++) {
for(int j=0; j<=i; j++) {
result[index++] = triangle[i][j];
}
}
return result;
}
}
2) dx, dy로 방향을 정하는 방법
- dx,dy는 각각 'x의 변화량'과 'y의 변화량'이라는 의미이다.
- '변화량'은 특정 방향으로 이동할 때 해당 좌표 값이 어떻게 변화하는지를 의미
(x,y)의 상하좌우로의 좌표 변화량
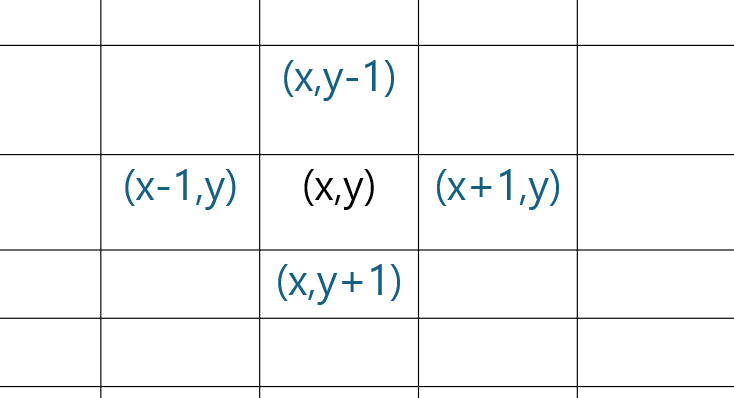
- dx,dy는 x,y 좌표의 변화량이므로 상하좌우 네 방향에서 대해서는 다음 값을 가진다.
| 상 | 하 | 좌 | 우 | |
| dx | 0 | 0 | -1 | 1 |
| dy | -1 | 1 | 0 | 0 |
- 여러 개의 방향을 다루기 위해 이 값을 배열에 담으면 dx,dy 변수가 된다.
- 위 표를 그대로 배열로 옮겼으니 배열의 인덱스가 방향이 된다.
private static final int[] dx = {0,0,-1,1};
private static final int[] dy = {-1,1,0,0};
더 나은 문제 풀이
삼각 달팽이 문제에서 사용되는 dx,dy
| 아래 | 오른쪽 | 왼쪽 위 | |
| dx | 0 | 1 | -1 |
| dy | 1 | 0 | -2 |
private static final int[] dx = {0,1,-1};
private static final int[] dy = {1,0,-1};
- 배열 인덱스는 방향을 나타낸다. 이 방향은 숫자를 채워 나감에 따라 변화므로 위치 변수와 함께 방향 변수를 추가한다.
...
int x = 0;
int y = 0;
int d = 0; //방향 변수
...
- 무한 루프 안에서 다음과 같이 triangle에 숫자를 채워준다.
triangle[y][x] = v++;
- 숫자를 채웠으니 진행 방향으로 이동해야 한다. 진행 방향은 d 변수에 저장되어 있으므로 다음 위치는 코드처럼 계산 가능
int nx = x+dx[d];
int ny = y+dy[d];
- dx,dy를 이용하여 모든 방향에 적용할 수 있는 로직을 작성하고 있으므로 더 이상 진행할 수 없다는 것을 다음 코드로 검사 가능하다.
if(nx == n || ny==n || nx==-1 || ny==-1 || triangle[ny][nx] !=0) {
}
- 아래 방향이나 오른쪽으로 진행할 때를 위한 nx == n || ny == n 조건
- 왼쪽 위로 진행할 때를 위한 nx == -1 || ny == -1 조건
- 이미 숫자가 써 있는 칸에 도달했음을 검사하는 triangle[ny][nx] != 0 조건
- 방향 변수 d의 값을 1 증가시키는 것으로 방향으로 바꿀 수 있다. 또 방향 개수가 3개이므로 나머지 연산을 이용하여 왼쪽 위 방향에서 아래 방향으로 전환될 수 있게 한다.
- 2를 넘어가면 다시 0으로 돌아오게 한느 것은 나머지 연산자를 이용하여 다음과 같이 작성 가능하다.
d = (d+1)%3;
- 전환된 방향을 이용하여 다음 위치를 계산할 수 있다.
nx = x + dx[d];
ny = y + dy[d];
- 전환된 방향으로도 진행을 못하는 경우가 있다. 바로 모든 숫자가 다 채워졌을 때이다. 이 경우에는 break를 이용하여 숫자 채우기를 종료 한다.
if(nx == n || ny==n || nx==-1 || ny==-1 || triangle[ny][nx] !=0) break;
- if문이 종료되고 나면 nx,ny에는 진행할 수 있는 방향 위치가 들어있다. if문 이후에 다음과 같아 현재 위치를 업데이트
x = nx;
y = ny;
전체 코드
class Solution {
private static final int[] dx = {0,1,-1};
private static final int[] dy = {1,0,-1};
public int[] solution(int n) {
int triangle[][] = new int[n][n];
int v = 1;
int x = 0;
int y = 0;
int d = 0; //방향 변수
while(true) {
triangle[y][x] = v++;
int nx = x +dx[d];
int ny = y +dy[d];
//막혔을 때
if(nx == n || ny == n || nx == -1 || ny == -1 || triangle[ny][nx] != 0) {
//방향 전환
d = (d+1)%3;
nx = x + dx[d];
ny = y + dy[d];
//숫자 다 채웠을 때
if(nx == n || ny == n || nx == -1 || ny == -1 || triangle[ny][nx] != 0) break;
}
//현재 위치 업데이트
x = nx;
y = ny;
}
int result[] = new int[v-1];
int index = 0;
for(int i=0; i<n; i++) {
for(int j=0; j<=i; j++) {
result[index++] = triangle[i][j];
}
}
return result;
}
}'Java > 알고리즘' 카테고리의 다른 글
| [PCCP 대비] ch 4. 문자열 (1) (0) | 2024.11.24 |
|---|---|
| [PCCP 대비] ch 3 배열 (2) (1) | 2024.11.23 |
| [자바 알고리즘 인터뷰] 12장 그래프 (9) 코스 일정 (0) | 2024.05.18 |
| [자바 알고리즘 인터뷰] 12장 그래프 (8) 여행 경로 (0) | 2024.05.18 |
| [자바 알고리즘 인터뷰] 12장 그래프 (7) 일정 재구성 (0) | 2024.05.17 |


