1.3 더블 링크드 리스트
더블 링크드 리스트 (Doubly Linked List)
- 링크드 리스트의 탐색 기능을 개선한 자료구조
- 더블 링크드 리스트에서는 양방향으로 탐색 가능
- 더블 링크드 리스트의 노드는 자신 앞에 있는 노드를 가리키는 포인터도 갖고 있음

- 더블 링크드 리스트의 노드
Typedef int ElementType;
typedef struct tagNode
{
ElementType Data;
struct tagNode* PrevNode; //이전 노드를 가리키는 포인터
struct tagNode* NextNode; //다음 노드를 가리키는 포인터
}Node;
1.3.1 더블 링크드 리스트의 주요 연산
1) 노드 생성/소멸 연산
노드 생성 함수 DLL_CreateNode()
Node* DLL_CreateNode( ElementType NewData)
{
Node* NewNode = (Node*)malloc(sizeof(Node));
NewNode->Data = NewData;
NewNode->PrevNode = NULL;
NewNode-> NextNode = NULL;
return NewNode;
}
노드 삭제 함수 DLL_DestroyNode(Node* Node)
Void DLL_DestroyNode(Node* Node)
{
free(Node);
}
2) 노드 추가 연산
- 기존 테일의 NextNode 포인터가 새로 추가된 테일을 가리키도록 함
- 새로운 테일의 PrevNode 포인터도 기존 테일의 주소를 가리키도록 해야함
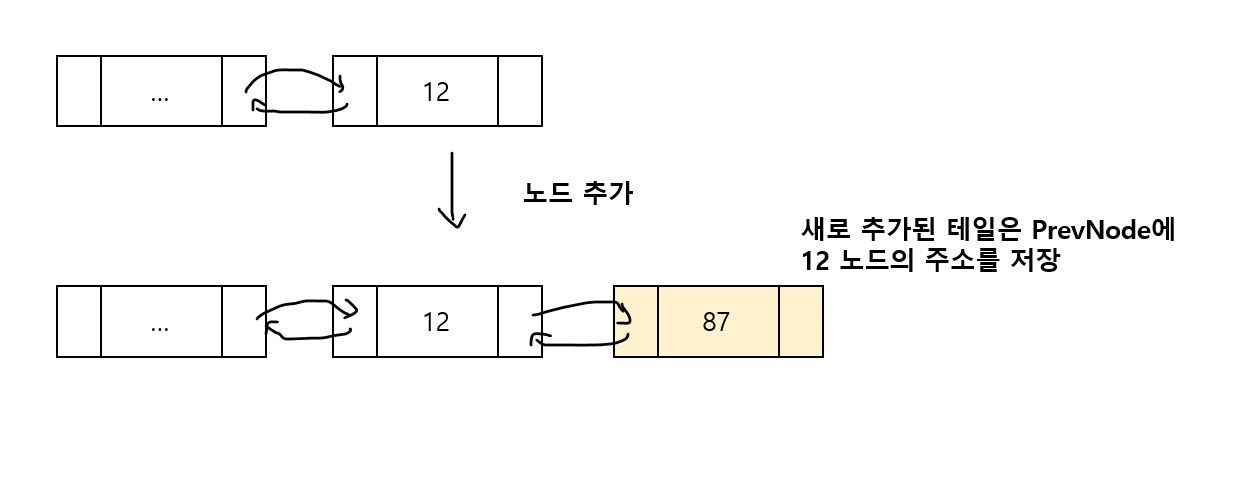
노드 추가 함수 DDL_AppendNode()
Void DLL_AppendNode( Node** Head, Node* NewNode)
{
//헤드 노드가 NULL이라면 새로운 노드가 Head가 된다
if( (*Head) == NULL)
{
*Head = NewNode;
}
else
{
//테일을 찾아 NewNode를 연결
Node*Tail = (*Head);
while( Tail->NextNode != NULL)
{
Tail = Tail->NextNode;
}
Tail->NextNode = NewNode;
NewNode->PrevNode = Tail; //기존의 테일을 새로운 테일의 PrevNode가 가리킴
}
}
3) 노드 탐색 연산
- 노드 탐색 함수 DLL_GetNodeAt()
Node* DLL_GetNodeAt(Node* Head, int Location)
{
Node* Current = Head;
while ( Current != NULL && (--Location) >= 0 )
{
Current = Current->NextNode;
}
return Current;
}
4) 노드 삭제 연산
- 삭제할 노드의 NextNode 포인터가 가리키던 노드를 이전 노드의 NextNode 포인터가 가리키게 바꿈
- 삭제할 노드의 PrevNode 포인터가 가리키던 노드를 다음 노드의 PrevNode 포인터가 가리키게 바꿈
- 삭제할 노드의 NextNode와 PrevNode는 NULL로 초기화
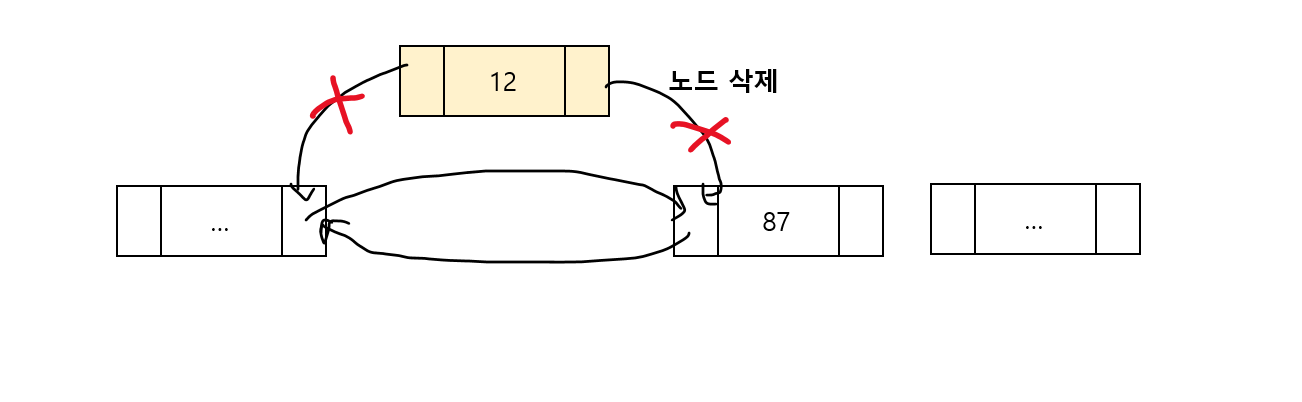
노드 삭제 함수 DDL_RemoveNode()
Void DLL_RemoveNode(Node** Head, Node* Remove)
{
if(*Head == Remove)
{
*Head = Remove-> NextNode;
if( (*Head) != NULL)
(*Head)->PrevNode = NULL;
Remove->PrevNode = NULL;
Remove->NextNode = NULL;
}
else
{
Node* Temp = Remove;
if( Remove->PrevNode != NULL)
Reomve->PrvNode->NextNode = Temp->NextNode;
if( Remove-> NextNode != NULL)
Remove->NextNode->PrevNode = Temp->PrevNode;
Remove->PrevNode = NULL;
Remove->NextNode = NULL;
}
}
5) 노드 삽입 연산
- 새로운 노드를 삽입할 때 PrevNode 포인터로는 이전 노드를, NextNode포인터로는 다음 노드를 가리키게 함
- 이전 노드의 NextNode 포인터와 다음 노드의 PrevNode 포인터는 새 노드를 가리키게 함

노드 삽입 함수 DLL_InsertAfter()
void DLL_InsertAfter( Node* Current, Node* NewNode)
{
NewNode->NextNode = Current->NextNode;
NewNode->PrevNode = Current;
if( Current->NextNode != NULL)
{
Current->NextNode->PrevNode = NewNode;
Current->NextNode = NewNode;
}
}
6) 노드 개수 세기 연산
노드 개수 세기 함수 DLL_GetNodeCount( Node* Head)
Int DLL_GetNodeCount(Node* Head)
{
unsigned int Count=0;
Node* Current = Head;
while( Current != NULL)
{
Current = Current->NextNode;
Count++;
}
return Count;
}
1.4 환형 링크드 리스트
환형 링크드 리스트 (Circular Linked List)
- 머리(Head)가 꼬리(Tail)를 물고 있는 형태의 링크드 리스트
- 헤드는 자신의 이전 노드로 테일을 가리킴
- 테일은 자신의 다음 노드로 헤드를 가리킴
- "시작을 알면 끝을 알 수 있고, 끝을 알면 시작을 알 수 있다"

1.4.1 환형 더블 링크드 리스트의 주요 연산
1) 노드 추가 연산
- 비어 있는 리스트에 새 노드 추가
- 새로운 노드는 헤드가 되고 헤드의 이전 노드는 헤드가 되며 헤드의 다음 노드는 헤드 자신이 됨
- 비어 있지 않는 리스트에 새 노드 추가
- '테일 노드 뒤에 새 노드를 붙인다'보다 '테일과 헤드 사이에 새 노드를 삽입한다'
노드 추가 함수 CDLL_AppendNode()
void CDLL_AppendNode(Node** Head, Node* NewNode)
{
//헤드 노드가 NULL이라면 새로운 노드가 Head가 됨
if( (*Head) == NULL)
{
*Head = NewNode;
(*Head)-> NewNode = *Head;
(*Head)-> PrevNode = *Head;
}
else
{
//테일과 헤드 사이에 NewNode 삽입
Node* Tail = (*Head)->PrevNode;
Tail->NextNode->PrevNode = NewNode;
Tail->NextNode = NewNode;
NewNode->NextNode = (*Head);
NewNode->PrevNode = Tail; //새로운 테일의 PrevNode가 기존의 테일을 가리킴
}
}
2) 노드 삭제 연산
노드 삭제 함수 CDLL_RemoveNode()
void CDLL_RemoveNode(Node** Head, Node* Remove)
{
if(*Head == Remove)
{
//꼬리 노드의 다음 노드를 삭제 노드의 다음노드로 지정
(*Head)->PrevNode->NextNode = Remove->NextNode;
//머리 노드의 다음노드의 이전 노드를 삭제 노드의 이전드로 지정
(*Head)->NextNode->PrevNode = Remove->PrevNode;
*Head = Remove->NextNode;
Remove->PrevNode = NULL;
Remove->NextNode = NULL;
}
else
{
Remove->PrevNode->NextNode = Remove->NextNode;
Remove->NextNode->PrevNode = Remove->PrevNode;
Remove->PrevNode = NULL;
Remove->NextNode = NULL;
}
}
'C언어 > 알고리즘' 카테고리의 다른 글
| [자료구조] ch 4 트리 (1) - 이진 트리 (2) | 2023.09.18 |
|---|---|
| [자료구조] ch 3. 큐 (0) | 2023.09.18 |
| [자료구조] ch 2. 스택(2) - 사칙 연산 계산기 (0) | 2023.09.15 |
| [자료구조] ch 2. 스택 (1) (0) | 2023.09.14 |
| [자료구조] ch 01 리스트 (1) (0) | 2023.09.11 |



