https://www.acmicpc.net/problem/11660
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
- N*N개의 수가 N*N 크기의 표에 채워져 있다. (x1,y1)부터 (x2,y2)까지 합을 구하는 프로그램
- (x,y)는 x행 y열을 의미
- N=4일 때 (2,2)부터 (3,4)까지 합 3+4+5+4+5+6 = 27

문제 풀이
2차원 누적합
[Algorithm] 2차원 배열 부분합, 누적합 구하기 (velog.io)
[Algorithm] 2차원 배열 부분합, 누적합 구하기
출처. 2차원 누적합, 부분합 구하기2차원배열에서 부분 배열의 합을 구하는 방법을 알아보자. 이중 for를 이용해서 구할 수 있지만 시간복잡도가 O(n^2)이 되기 때문에 더 효율적인 방법을 찾아보
velog.io
- 이차원 배열에 대한 누적합 배열 또한 2차원 배열이 된다.
- 직사각형 형태의 배열에 포함되는 직사각형 구간의 원소의 합을 빠르게 구할 수 있다.
- 이차원 배열 a(1,1)이라 할 때, 누적합 배열 S(i,j)가 있다고 가정
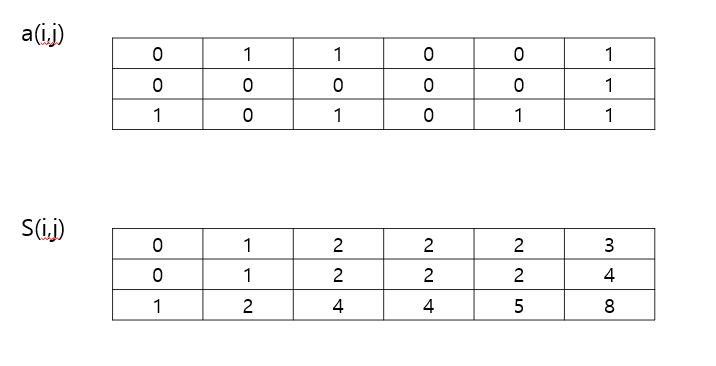
- 좌측 상단을 a(1,1)이라 할 때, a(1,1)과 a(i,j)를 양 대각 끝 꼭짓점으로 하는 직사각형 범위 면적 안의 모든 a 원소의 합으로 정의
- 따라서 a(2,2) ~ a(3,3)의 부분합을 구해보자
- S(3,3)값에서 S(1,3) 값을 빼고 S(3,1)값을 뺀다. 이때 S(1,1)은 S(1,3)과 S(3,1)에 의해서 2번 빼진 셈이니 S(1,1)을 더해주면 초록색 부분의 구간합이 된다.

- 2차원 배열 arr이 있을 때 arr[x1][x2] 부터 arr[x2][y2]까지의 부분 배열의 합을 Range(x1,y1,x2,y2)라고 하자.
- 그리고 누적합 배열 S로 다음과 같이 정의된다.
Range(x1,y1,x2,y2) = S(x2,y2) - S(x1,y2) - S(x2,y1) + S(x1,x1)
- a(i,j)에서 행방향으로 누적합을 구한다.
- 행 누적합에 대해서 열방향으로 누적합을 구한다.
정답
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int prefixSum[][] = new int[n+1][n+1];
for(int i=1; i<=n; i++)
{
st= new StringTokenizer(br.readLine());
for(int j=1; j<=n; j++)
{
prefixSum[i][j] = prefixSum[i][j-1] + prefixSum[i-1][j]-prefixSum[i-1][j-1]+ Integer.parseInt(st.nextToken());
}
}
for(int i=0; i<m; i++)
{
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
sb.append(prefixSum[x2][y2] - prefixSum[x2][y1-1] - prefixSum[x1-1][y2]+prefixSum[x1-1][y1-1]).append("\n");
}
System.out.println(sb);
}
}

'Java > 백준' 카테고리의 다른 글
| [JAVA] 백준 1931 회의실 배정 (1) | 2024.03.04 |
|---|---|
| [JAVA] 백준 11047 동전 0 (0) | 2024.03.03 |
| [JAVA] 백준 10986 나머지 합 (0) | 2024.03.02 |
| [JAVA] 백준 2559 수열 (0) | 2024.03.01 |
| [JAVA] 백준 11659 구간 합 구하기 4 (0) | 2024.02.29 |



