https://www.acmicpc.net/problem/11049
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
- 크기가 N*M인 행렬 A와 M*K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N*M*K번이다.
- 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.
- 예를 들어, A의 크기가 5*3이고, B의 크기가 3*2, C의 크기가 2*6인 경우의 행렬의 곱 ABC를 구하는 경우를 생각해보자.
1) AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5*3*2 + 5*2*6 = 30+60 = 90번이다.
2) BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3*2*6 + 5*3*6 = 36 + 90 = 126번이다.
- 같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.
- 행렬 N개의 크기가 주어졌을 떄, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램
- 입력으로 주어진 행렬의 순서를 바꾸면 안된다.
문제 풀이
연속 행렬 곱셈 문제 (Chained Matrix Multiplications)
- 연속된 행렬들의 곱셈에 필요한 원소 간의 최소 곱셈 횟수를 찾는 문제
- 연속된 행렬의 곱샘에는 결합 법칙이 허용된다. 즉 A*B*C = (A*B)*C = A*(B*C) 이다.
- 주어진 행렬의 순서를 지켜서 이웃하는 행렬을 반드시 곱해야 하기 때문에 다음과 같은 부분 문제들이 만들어 진다.
ex) A*B*C*D*E

- 맨 윗줄의 가장 작은 부분문제들은 입력으로 주어진 각각의 행렬 그 자체이고, 크기가 2인 부분문제는 2개의 이웃하는 행렬의 곱셈으로 이루어진 4개이다.
- 주목할점은 부분문제들이 겹쳐져 있다는 것이다. 만일 A*B, C*D와 같이 부분문제가 서로 겹치지 않으면 A*B*C*D를 계산할 때 B*C에 대한 해가 없으므로 새로이 계산해야 한다. 이러한 경우를 대비하여 이웃하여 서로 겹치는 부분문제들의 해도 미리 구하여 놓는다.
입력: 연속된 행렬 A1 * A2* ... *An,
단, A1은 d0*d1. A2는 d1*d2, ... , An은 dn-1*dn이다.
출력: 입력의 행렬 곰셈에 필요한 원소 간의 최소 곱셈 횟수
1)for i=1 to n
2) C[i,i] = 0
3)for L=1 to n-1 {
4) for i=1; to n-L {
5) j=i+L
6) c[i,j] = ∞
7) for k=i to j-1 {
8) temp - C[i,k]+C[k+1,j] + di-1dkdj
9) if(temp < C[i,j])
10) C[i,j] = temp
}
}
}
return C[1,n]
1,2)
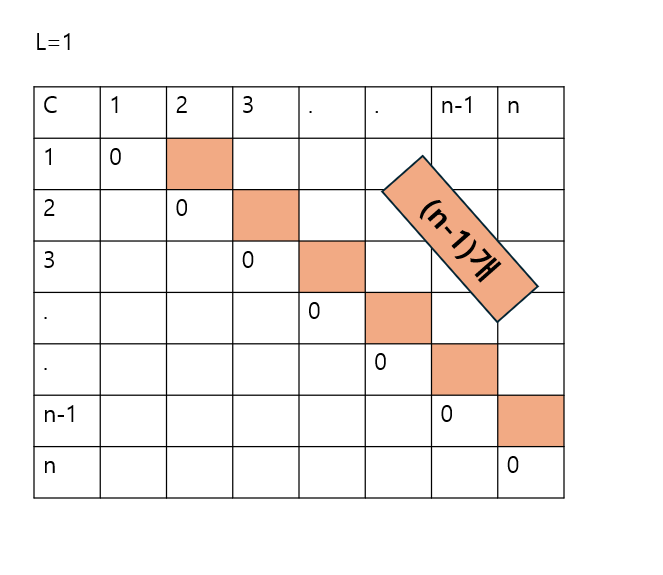
- 배열의 대각선 원소들을 0으로 각각 초기화
- 그 의미는 행렬 A1*A1, A2*A2, ...,An*An을 각각 계산하는 데 필요한 원소 간의 곱셈 횟수가 0이라는 뜻
- 초기화 하는 이유는 C[i,j]가 가장 작은 부분 문제의 해이기 때문
3)
- for 루프의 L은 1부터 (n-1)까지 변하는데, L은 부분문제의 크기를 2부터 n까지 조절하기 위한 변수이다.
- 이를 위해 4)의 for 루프가 i가 1부터 (n-L)까지 변한다.
L=1 -> i는 1부터 (n-1)까지 변함 -> 크기가 2인 부분문제의 수가 (n-1)개
L=2 -> i는 1부터 (n-2)까지 변함 ->크기가 3인 부분 문제의 수가 (n-2)개
L=3 -> i는 1부터 (n-3)까지 변함 -> 크기가 4인 부분문제의 수가 (n-3)개
L=n-2 -> i는 1부터 n-(n-2) = 2까지 변함 -> 크기가 (n-1)인 부분 문제의 수가 2
L=n-1 -> i는 1부터 n-(n-1) =1까지 변함 -> 크기가 n인 문제의 입력
5)
- j=i+L은 행렬 Ai* ... *Aj에 대한 원소 간의 최소 곱셈 횟수 , 즉 C[i,j]를 계산하기 위한 것
L=1일때,
i=1 -> j=1+1=2 -> A1*A2를 계산하기 위함
i=2 -> j=2+1=3 -> A2*A3를 계산하기 위함
i=3 -> j=3+1=4 -> A4*A4를 계산하기 위함
..
L= n-L = n-1 -> j=(n-1)+1=n -> An-1*An을 계산하기 위함
-> 크기가 2인 부분문제의 수가 총 (n-1)개
L=2일때,
i=1 -> j=1+2=3 -> A1*A2*A3를 계산하기 위함
i=2 -> j=2+2=4 -> A2*A3*A4를 계산하기 위함
i=3 -> j=3+2=5 -> A3*A4*A5를 계산하기 위함
..
L= n-L = n-2 -> j=(n-2)+2=n -> An-2*An-1*An을 계산하기 위함
-> 크기가 3인 부분문제의 수가 총 (n-2)개
L=n-2일 때, 2개의 부분 문제 A1*A2*....*An-1, A2*A3*...*An을 계산
L=n-1일 떄, i=1이면 j=1+(n-1) = n이고, 주어진 문제 입력인 A1*A2* ... * An을 계산
6)
- 최소 곱셈 횟수를 찾기 위해 C[i,j] = 무한대로 초기화
7~10)
- k가 i부터 (j-1)까지 변하면서 어떤 부분문제를 먼저 계산하면 곱셈 횟수가 최소인지를 찾아서 최종적으로 C[i,j]]에 그 값을 저장한다.
- 다음과 같이 k가 Ai*Ai+1* ... * Aj를 2개의 부분문제로 나누어 어떤 경우에 곱셈 횟수가 최소인지를 찾음

8)
- 앞과 같이 2개의 부분 문제로 나뉜 각각의 경우에 대한 곱셈 횟수를 계산
- 첫 번째 부분문제의 해는 C[i,k]에 있고, 두 번째 부분문제의 해는 C[k+1, j]에 있으며, 이 2개를 합하고, 이에 di-1dkdj를 더한다.
- di-1dkdj를 더하는 이유는 두 부분문제들이 각각 di-1*dk 행렬과 dk*dj 행렬이고, 이 두행렬을 곱하는 데 필요한 원소 간의 곱셈 횟수가 di-1dkdj이기 때문이다.

9~10)
- 앞에서 계산된 곱셈 횟수가 바로 직전까지 계산되어 있는 C[i,j]보다 작으면 그 값으로 C[i.j]를 갱신하며 k=(j-1)일 떄까지 수행되어 최종적으로 가장 작은 값이 C[i,j]에 저장
11)
- 주어진 문제의 해가 있는 C[1,n]을 리턴
[백준(Baekjoon)][자바(java)] 11049 : 행렬 곱셈 순서 / 동적 계획법 2 (tistory.com)
[백준(Baekjoon)][자바(java)] 11049 : 행렬 곱셈 순서 / 동적 계획법 2
www.acmicpc.net/problem/11049 11049번: 행렬 곱셈 순서 첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서
hyunjiishailey.tistory.com
정답
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;
public class Main
{
public static void main(String[] args) throws IOException
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
int data[] = new int[N+1];
for(int i=0; i<N; i++)
{
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j=0; j<2; j++)
{
data[i+j] = Integer.parseInt(st.nextToken());
}
}
int memo[][] = new int[N+1][N+1];
for(int L=0; L<N; L++)
{
for(int i=1; i<N-L; i++)
{
int j= i+L+1;
memo[i][j] = Integer.MAX_VALUE;
for(int k=i; k<j; k++)
{
memo[i][j] = Math.min(memo[i][j],memo[i][k]+memo[k+1][j]+(data[i-1]*data[k]*data[j]));
}
}
}
bw.write(String.valueOf(memo[1][N]));
bw.flush();
bw.close();
}
}

'Java > 백준' 카테고리의 다른 글
| [JAVA] 백준 24445 알고리즘 수업 - 너비 우선 탐색 2 (1) | 2024.04.03 |
|---|---|
| [JAVA] 백준 24444 알고리즘 수업 - 너비 우선 탐색 1 (0) | 2024.04.02 |
| [JAVA] 백준 11066 파일 합치기 (1) | 2024.03.22 |
| [JAVA] 백준 12015 가장 긴 증가하는 부분 수열 2 (0) | 2024.03.21 |
| [JAVA] 백준 1450 냅색문제 (0) | 2024.03.20 |



