https://leetcode.com/problems/longest-palindromic-substring/description/

- 가장 긴 팰린드롬 부분 문자열을 출력하라
풀이 1) 팰린드롬을 발견하면 확장하는 풀이
최장 공통 부분 문자열(Longest Common Substring)
- 여러 개의 입력 문자열이 있을 때 서로 공통된 가장 긴 부분 문자열을 찾는 문제로, 다이나믹 프로그래밍으로 풀 수 있는 전형적인 문제
- 이 문제 또한 동일한 유형의 문제로서, 동일하게 다이나믹 프로그래밍으로 풀 수있다.
- 그러나 이 문제의 경우 다이나믹 프로그래밍을 이용한 풀이는 직관적으로 이해가 어렵고, 실행속도가 느리다.
- 그러므로 투 포인터(Tow Pointers)가 팰린드롬을 발견하면 확장하는 형태로 풀이
- 팰린드롬 판별만 하면 된다는 점에서 착안해서, 매칭이 될 때 중앙을 중심으로 점점 확장해나가면서 가장 긴 팰린드롬을 판별하는 알고리즘
- 2칸, 3칸으로 구성된 투포인터가 슬라이딩 윈도우처럼 계속 앞으로 전진해 나간다.
- 이때 윈도우에 들어온 문자열이 팰린드롬인 경우 그 자리에 멈추고, 투 포인터는 점점 확장하는 식이다.
- 팰린드롬은 dd처럼 짝수(2칸)일 때도 있고, bab처럼 홀수(3칸)일 때도 있다.
- 따라서 짝수나 홀수 모든 경우에 대해 판별한다.
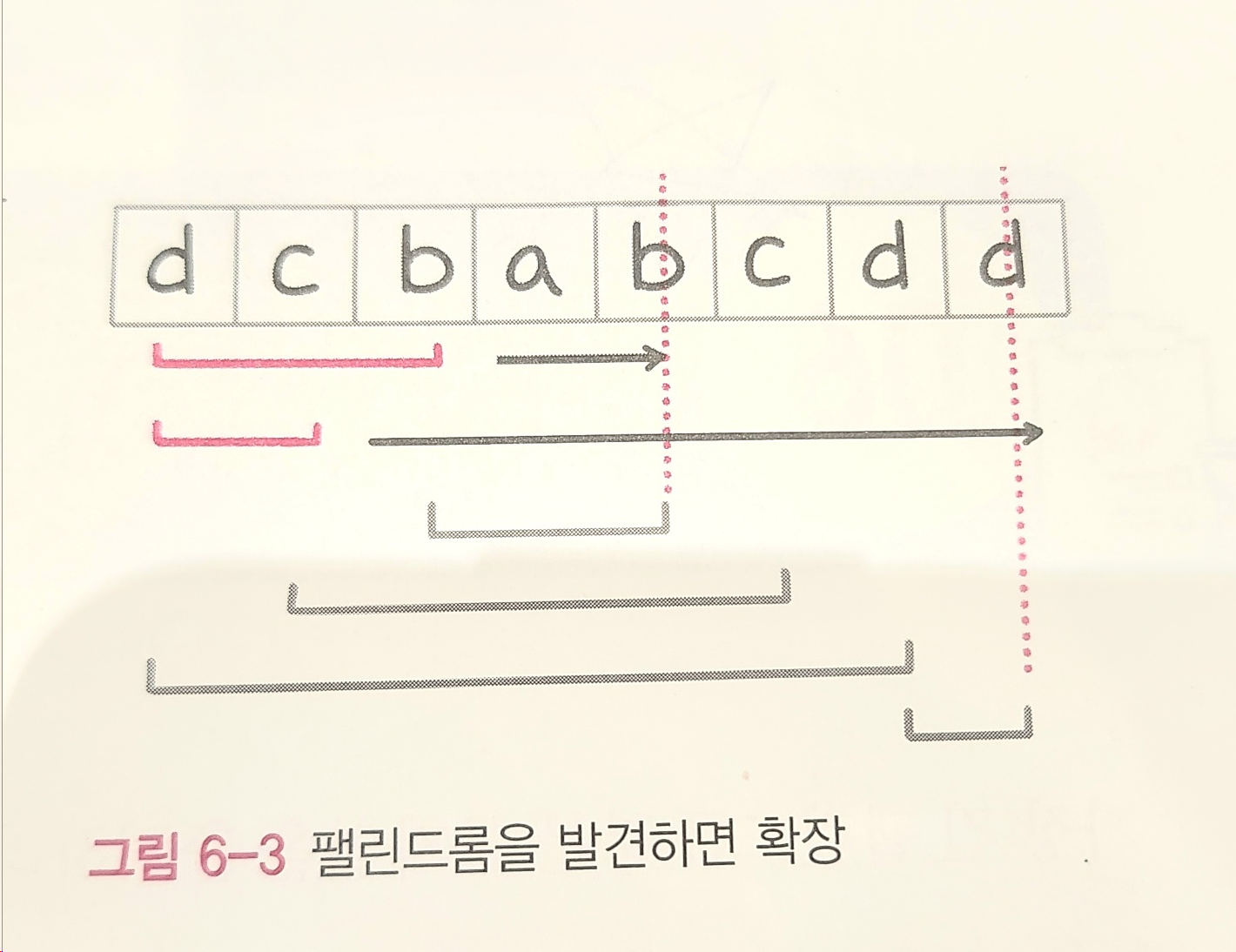
- 2개의 투 포인터가 계속 우측으로 이동하다 3칸짜리 투포인터는 bab에서 앞뒤 b가 팰린드롬으로 매칭이 되어 cbabc, dcbabcd까지 확장되면서 가장 긴 값으로 저장된다.
- 이 외에 2칸짜리 투 포인터도 마지막 부분에서 dd에 매칭되지만 마지막 문자이기 때문에 오른쪽 방향으로는 더 이상 확장되지 못하고 그대로 종료된다.
- 그래서 정답은 dcbabcd가 된다.
class Solution {
int left, maxLen;
public void extendPalindrome(String s, int j, int k)
{
//투포인터가 유효한 범위 내에 있고, 양쪽 끝 문자가 일치하는 팰린드롬인 경우 범위 확장
while(j>=0 && k<s.length()&&s.charAt(j) == s.charAt(k)) {
j--;
k++;
}
//기존 최대 길이보다 큰 경우 값 교체
if(maxLen<k-j-1){
left = j+1;
maxLen = k-j-1;
}
}
public String longestPalindrome(String s) {
//문자 길이 저장
int len = s.length();
//길이가 1인 경우 예외 처리
if(len <2) return s;
//우측으로 한 칸씩 이동하면서 투 포인터 조사
for(int i=0; i<len-1; i++)
{
extendPalindrome(s,i,i+1); //2칸짜리 투 포인터
extendPalindrome(s,i,i+2); //3칸짜리 투 포인터
}
//왼쪽과 최대 길이만큼을 더한 오른쪽만큼의 문자를 정답으로 리턴
return s.substring(left, left+maxLen);
}
}
실핵시간 : 22밀리초
'Java > 알고리즘' 카테고리의 다른 글
| [자바 알고리즘 인터뷰] 7장 배열 (2) 빗물 트래핑 (1) | 2024.04.05 |
|---|---|
| [자바 알고리즘 인터뷰] 7장 배열 (1) 두 수의 합 (0) | 2024.04.05 |
| [자바 알고리즘 인터뷰] 6장 문자열 처리(5) 그룹 애너그램 (0) | 2024.04.04 |
| [자바 알고리즘 인터뷰] 6장 문자열 처리(4) 가장 흔한 단어 (0) | 2024.04.04 |
| [자바 알고리즘 인터뷰] 6장 문자열 처리(3) 로그 파일 재정렬 (0) | 2024.04.04 |



