1. 재귀 알아보기
재귀적(recursive)
- 어떤 사건이 자기 자신을 포함하고 다시 자기 자신을 사용하여 정의
- 무한으로 존재하는 자연수의 재귀적 정의
1) 1은 자연수 입니다,
2) 자연수 n의 바로 다음 수도 자연수 입니다.
2. 순차곱셈 구하기
- 음이 아닌 정수의 순차곱셈(factorial)의 재귀적 정의
1. 0!=1
2. n>0이면 n!=n*(n-1)!
- 순차곱셈의 결과를 재귀적으로 구하여 출력
#include <stdio.h>
//정수 n의 순차곱셈값을 반환
int factorial(int n)
{
if(n>0)
return n*factorial(n-1);
else
return 1;
}
int main()
{
int x;
printf("정수를 입력하세요:");
scanf("%d",&x);
printf("%d의 순차곱셈값은 %d입니다.\n",x,factorial(x));
return 0;
}
factorial(3)의 재귀적 호출 (recursive call)
- 매개 변수에 3을 전달받아 3*factorial(2) 반환 (3*2)
- 매개 변수에 2를 전달받아 2*factorial(1) 반환 (2*1)
- 매개 변수에 1을 전달받아 1*factorial(0) 반환 (1*1)
- 호출된 factorial 함수는 매개변수 n에 전달받은 값이 0이므로 1 반환
직접 재귀 (direct)
- 자신과 같은 함수를 호출
간접 재귀 (indirect)
- 함수 x가 함수 y를 호출하고 다시 함수 y가 함수 x를 호출
3. 유클리드 호제법 알아보기
- 두 정수의 최대공약수(greatest common divisor)를 재귀적으로 구하는 알고리즘
- 두 정수를 직사각형의 두 변의 길이라 생각
ex) 각 변의 길이가 22,8인 직사각형
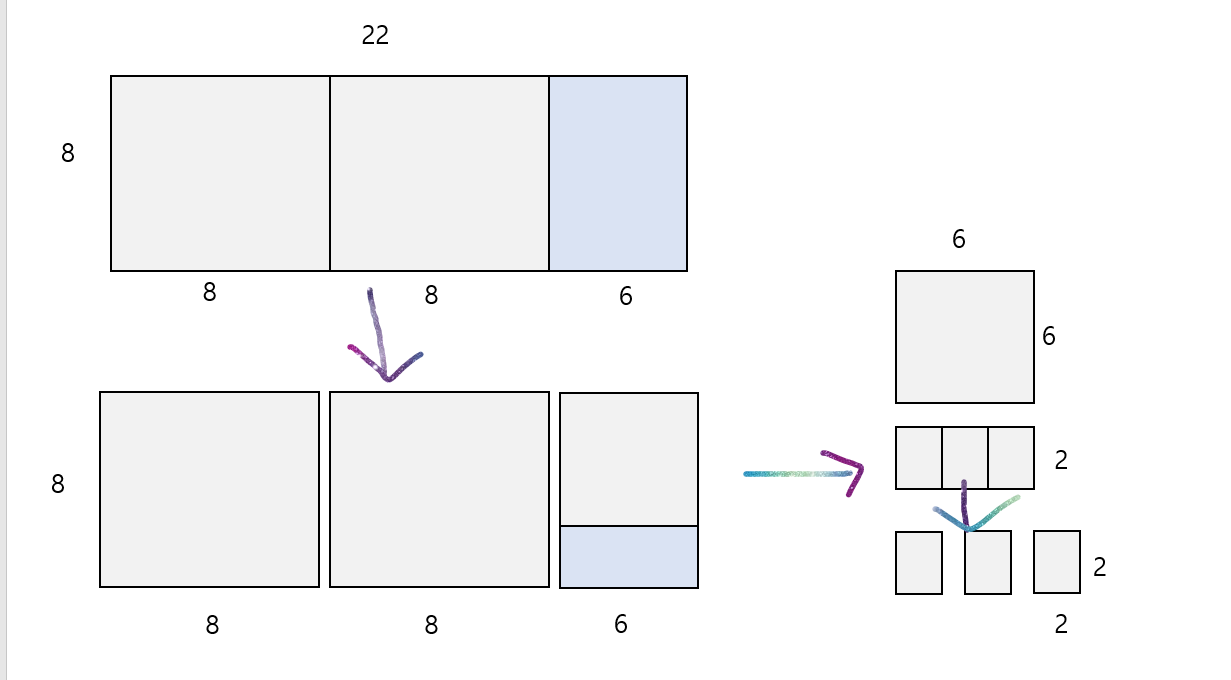
- 22*8크기의 직사각형에서 짧은 변(8)을 한변으로 하는 정사각형으로 분할
-> 8*6크기의 직사각형이 1개 남음
- 8*6크기의 직사각형을 짧은 변(6)을 한변으로 하는 정사각형으로 분할
-> 2*2크기의 정사각형 3개가 남음
-> 2가 최대 공약수
- 두 정수가 주어질 경우 큰 값을 작은 값으로 나누었을 때 나누어떨어지는 가장 작은값이 최대 공약수
- 나누어 지지 않으면 작은값(얻은 나머지)에 대해 나누어질때까지 같은과정을 재귀적으로 반복
- 유클리드 호제법에 의해 최대공약수를 구하여 출력
-> 최대공약수는 y가 0이면 x이고, y가 0이 아니면 gcd(y,x%y)로 구함
#include <stdio.h>
//정수 x,y의 최대공약수를 반환
int gcd(int x, int y)
{
if(y==0)
return x;
else
return gcd(y,x%y);
}
int main()
{
int x,y;
puts("두 정수의 최대공약수를 구합니다.");
printf("정수를 입력하세요:");
scanf("%d",&x);
printf("정수를 입력하세요:");
scanf("%d",&y);
printf("최대 공약수는 %d입니다.",gcd(x,y));
return 0;
}
'C언어 > 자료구조' 카테고리의 다른 글
| 5-3장 하노이의 탑 (0) | 2023.07.27 |
|---|---|
| 5-2 재귀 알고리즘 분석 (0) | 2023.07.27 |
| 4-2장 큐란? (0) | 2023.07.27 |
| 4-1 스택이란? (0) | 2023.07.26 |
| 함수 포인터 (0) | 2023.07.25 |



