1. 하노이의 탑 살펴보기
하노이의 탑 (Towers of Hanoi)
- 작은 원반이 위에, 큰 원반이 아래에 위치할 수 있도록 원반을 3개의 기둥 사이에서 옮기는 문제
- 모든 원반을 세번째 기둥으로 최소의 횟수로 옮김
- 원반은 1개씩만 옮길 수 있음
- 큰 원반을 작은 원반 위에 쌓을 수는 없음
- 원반이 3개일때 모든 과정

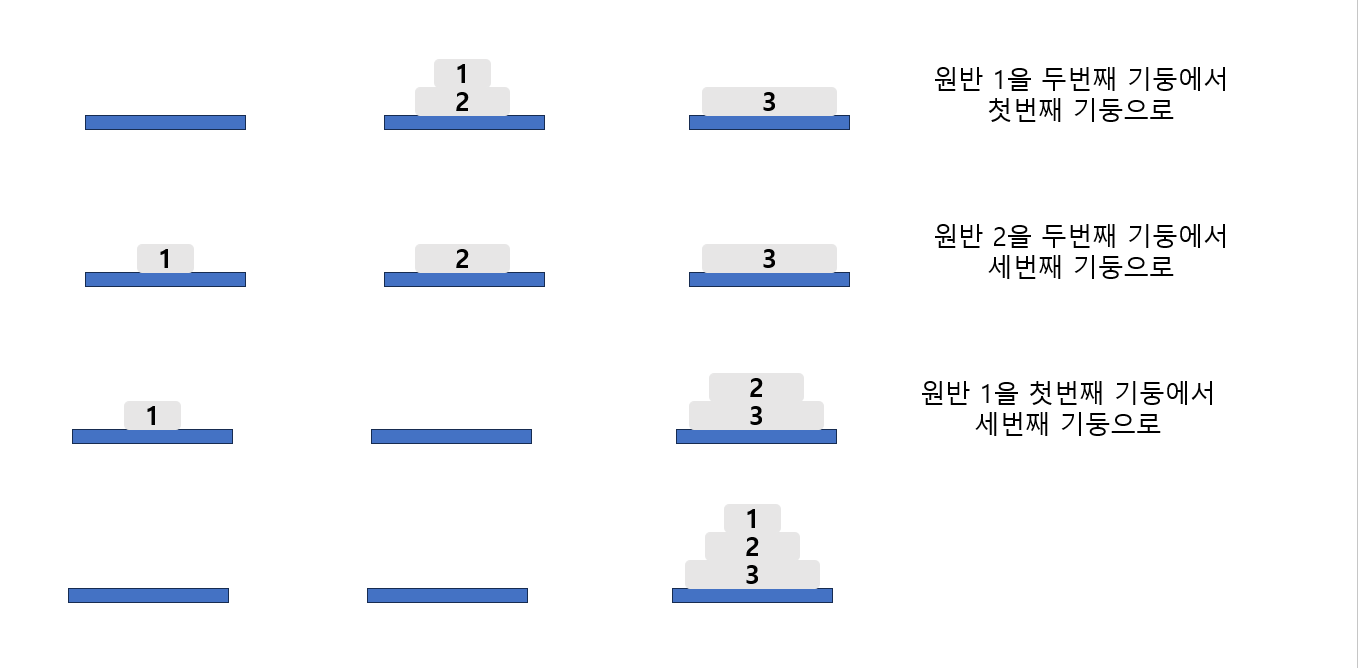
- 그룹 : 원반 1과 원반 2를 겹친 것
- 가장 큰 원반을 최소의 단계로 목표 기둥으로 옮기려면 먼저 '그룹'을 중간 기둥으로 옮겨야 함
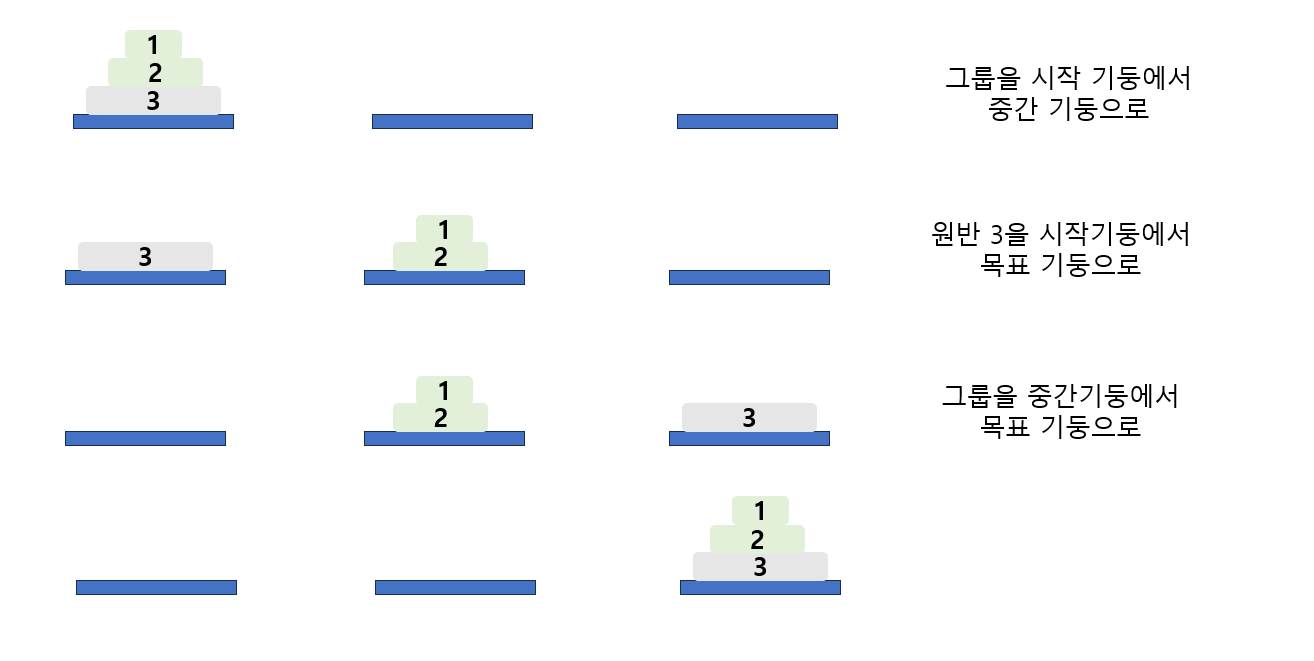
- 원반 1과 원반 2가 겹친 '그룹'을 옮기는 단계

- 하노이의 탑 구현 프로그램
- move( 옮겨야 할 원반의 개수, 시작 기둥의 번호, 목표 기둥의 번호)
//하노이의 탑
#include <stdio.h>
//원반[1] ~원반[no]를 x기둥에서 y기둥으로 옮김
void move(int no, int x, int y)
{
if(no>1)
move(no-1,x,6-x-y); //그룹을 시작기둥에서 중간 기둥으로
printf("원반[%d]를 %d기둥에서 %d 기둥으로 옮김\n",no,x,y); //바닥 원반을 목표 기둥으로
if(no>1)
move(no-1,6-x-y,y); //그룹을 중간 기둥에서 목표 기둥으로
}
int main(void)
{
int n; //원반의 개수
printf("하노이의 탑\n 원반 개수:");
scanf("%d",&n);
move(n,1,3);
return 0;
}
- 기둥 번호는 정수 1,2,3으로 나타냄
- 기둥 번호의 합이 6이므로 시작기둥, 목표 기둥이 어느 기둥이더라도 중간 기둥은 6-x-y로 구할 수 있음
1) 바닥 원반을 제외한 그룹(원반[1]~원반[no-1])을 시작 기둥에서 중간 기둥으로 옮김
2) 바닥 원반 no를 시작 기둥에서 목표 기둥으로 옮겼음을 출력
3) 바닥 원반을 제외한 그룹(원반[1]~원반[no-1])을 중간 기둥에서 목표 기둥으로 옮김
'C언어 > 자료구조' 카테고리의 다른 글
| 6-1장 정렬 (0) | 2023.07.28 |
|---|---|
| 5-4장 8퀸 문제 (0) | 2023.07.28 |
| 5-2 재귀 알고리즘 분석 (0) | 2023.07.27 |
| 5-1 재귀의 기본 (0) | 2023.07.27 |
| 4-2장 큐란? (0) | 2023.07.27 |


