5.1 탐색 알고리즘의 개요
- 탐색이란 '데이터를 찾는것'
- 자료구조 형태에 따라 사용할 수 있는 여러 가지 탐색 알고리즘
- 순차 탐색, 이진 탐색, 이진 탐색 트리, 레드 블랙 트리
5.2 순차 탐색
순차 탐색 (Sequential Search)
- 처음부터 끝까지 차례대로 모든 요소를 비교하여 원하는 데이터를 찾는 탐색 알고리즘
- 어느 한쪽 방향으로만 탐색할 수 있는 알고리즘이므로 선형 탐색(Linear Search)라고 부름
- 성능이 좋지 않지만, 정렬되지 않은 데이터에서 원하는 항목을 찾을 수 있는 유일한 방법이며 구현이 간단
- 극적으로 놓은 성능이 필요하지 않거나 데이터의 크기가 작은 상황에서 유용하게 활용
- 배열이나 링크드 리스트에 쉽게 적용할 수 있는 알고리즘
ex) 링크드 리스트를 위한 순차 탐색
Node* SLL_SequentialSearch(Node* Head, int Target)
{
Node* Current = Head;
Node* Match = NULL;
while(Current != NULL)
{
//찾고자 하는 값을 해당 노드가 갖고 있으면 노드의 주소를 Match에 저장
if(Current->Data == Target)
{
Match = Current;
break;
}
else
//현재 노드에 찾는 값이 없으면 다음 노드를 조사
Current = Current->NextNode;
}
return Match; //찾는 값을 갖고 있는 노드의 주소를 반환
}
자기 구성 순차 탐색(Self-Organizing Sequential Search)
- 자주 사용되는 항목을 데이터 앞쪽에 배치함으로서 순차 탐색의 검색 효율을 끌어올리는 방법
ex) 마트 매장 입구에 진열된 특별 행사 제품
MS 워드의 최근 문서 목록
배달 애플리케이션의 즐겨찾기
- 자주 사용되는 항목을 선별하는 방법에 따라 3가지로 나뉨
- 전진 이동법(Move To Front Method)
- 전위법 (Transpose Method)
- 빈도 계수법(Frequency Count Method)
5.2.1 전진 이동법
전진 이동법(move to Front Method)
- 탐색된 항목을 데이터의 가장 앞(링크드 리스트에서는 헤드)으로 옮기는 방법
- 전진 이동법을 사용하면 한 번 찾은 항목을 곧바로 다시 찾고자 할때 단번에 탐색 완료
- 한 번 탐색된 항목이 다음에 또 다시 검색될 가능성이 높은 데이터에 한해 사용
ex) MS 워드의 최근 문서 목록 기능
ex)
- 아래에 데이터에서 48 찾기

- 순차 탐색을 통해 여섯번째 요소에 담긴 48을 찾으면 이 요소를 뽑아 데이터의 가장 앞으로 이동시킴
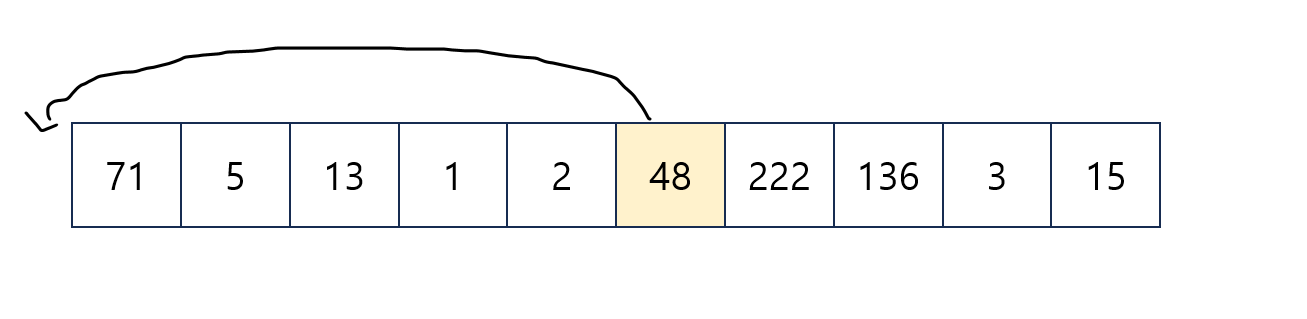
- 다음과 같이 데이터가 변경됨. 다음번에 48을 찾고자 할 때 첫 번째 요소에서 해당값을 바로 찾을 수 있음

- 링크드 리스트에 사용할 수 있는 전진 이동 순차 탐색법 구현
Node* SLL_MoveToFront(Node** Head, int Target)
{
Node* Current = (*Head);
Node* Previous = NULL;
Node* Match = NULL;
while( Current != NULL)
{
//찾고자 하는 값을 해당 노드가 갖고 있으면 노드의 주소를 Match에 저장
if( Current->Data == Target)
{
Match = Current;
if(Previous != NULL) //이전 노드가 비어있지 않으면
{
//자신의 이전노드와 다음 노드를 연결
Previous->NextNode = Current->NextNode;
//자신의 리스트의 가장 앞으로 옮기기
Current->NextNode = (*Head); //현재 노드의 다음 노드는 헤드
(*Head) = Current; //헤드가 현재 노드가 됨
}
break;
}
else // 타겟 노드와 일치하지 않다면
{
Previous = Current; //현재 노드는 이전 노드가 됨
Current = Current->NextNode; //현재 노드는 현재 노드의 다음 노드가 됨(한칸 이동)
}
}
return Match; //찾는 값을 가지고 있는 노드의 주소를 반환
}
5.2.2 전위법
전위법(Transpose Method)
- 탐색된 항목을 바로 이전 항목과 교환하는 전략을 취하는 알고리즘
- 전진 이동법은 탐색된 항목을 무조건 앞으로 옮기는 것에 비해, 전위법은 자주 탐색된 항목을 조금씩 앞으로 옮김
- 자주 탐색되는 항목들이 데이터 앞쪽으로 모이게 되고 ,이로 인해 자주 탐색되는 항목들을 빠르게 찾을 수 있게 됨
Node* SLL_Transpose(Node** Head, int Target)
{
Node* Current = (*Head);
Node* PPrevious = NULL; //이전 노드의 이전노드
Node* Previous = NULL; //이전 노드
Node* Match = NULL;
while( Current != NULL)
{
if(Current->Data == Target)
{
Match = Current;
if(Previous != NULL)
{
if(PPrevious != NULL)
PPrevious -> NextNode = Current;
else
(*Head) = Current;
Previous-> NextNode = Current->NextNode;
Current->NextNode = Previous;
}
break;
}
else
{
if(Previous != NULL)
PPrevious = Previous;
Previous = Current;
Current = Current->NextNode;
}
}
return Match;
}
5.2.3 계수법
계수법(Frequency Count Method)
- 데이터 내 각 요소가 탐색된 횟수를 별도의 공간에 저장해두고, 탐색된 횟수가 높은 순으로 데이터를 재구성하는 전략의 알고리즘
5.3 이진 탐색
이진 탐색(Binary Search)
- 정렬된 데이터에서 사용할 수 있는 '고속' 탐색 알고리즘
- 수행 과정
1) 데이터 중앙에 있는 요소를 고름
2) 중앙 요소값과 찾고자 하는 목표값을 비교
3) 목표값이 중앙 요소값보다 작다면 중앙을 기준으로 데이터 왼편에 대해, 크다면 오른편에 대해 이진 탐색을 새로 수행
4) 찾고자 하는 값을 찾을 때까지 1 ~3 단계 반복
ex)
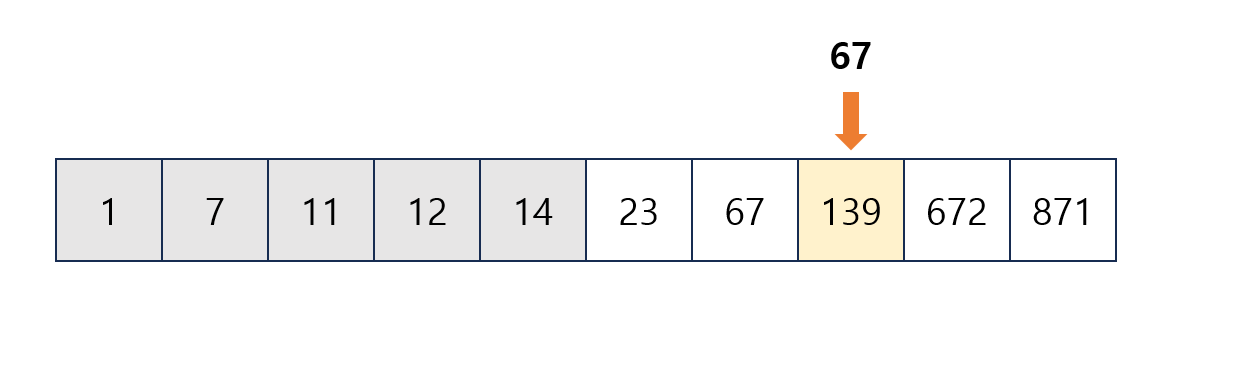
- 임의의 수 10개를 담고 있는 배열에서 67 찾기
- 중앙 요소의 위치 = 주어진 데이터의 크기를 반으로 나눔 =14
- 67이 14보다 크기 때문에 찾는 요소는 14를 기준으로 오른편에 있다는 사실을 알 수 있음

- 원래 데이터의 왼편을 탐색 대상에서 제외하고 오른편에서 다시 중앙 요소를 골라 비교
- 중앙 요소 139
- 67은 139보다 작으니까 왼편에 위치
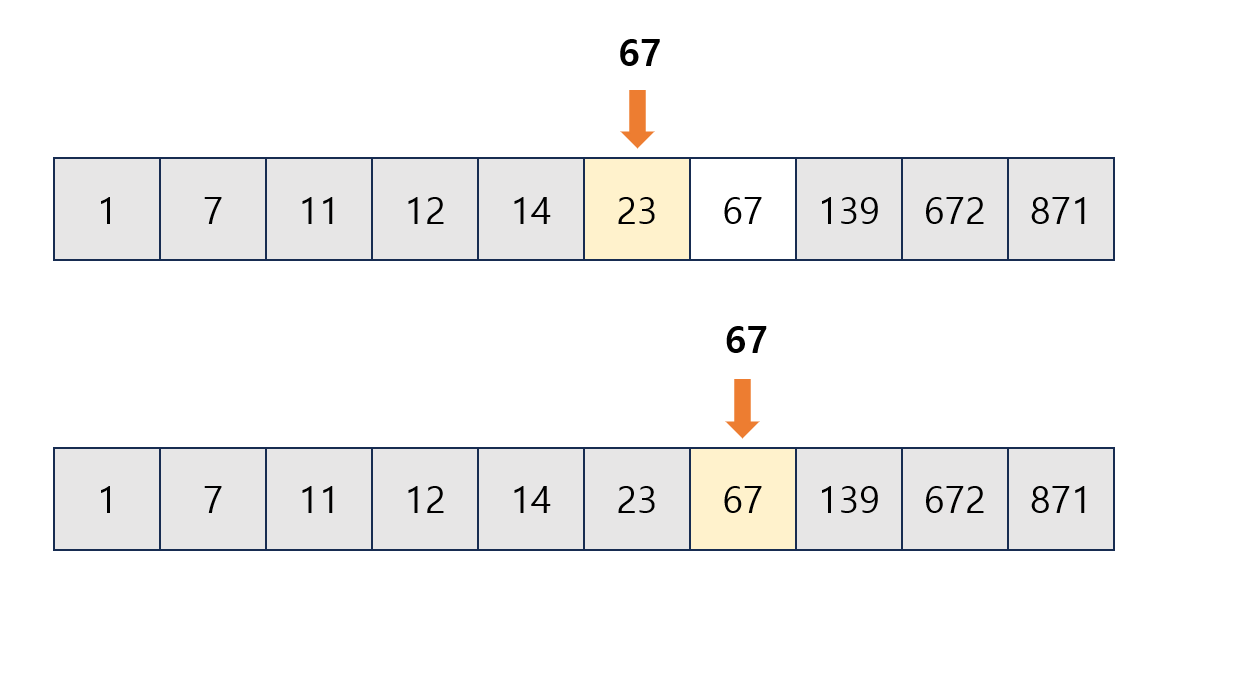
- 탐색 대상에서 제외된 요소들을 빼면 23과 67 둘만 남음
- 중앙 요소는 23이 되고 탐색 대상의 범위는 23의 오른쪽에 있는 67로 좁아짐
6.3.1 이진 탐색의 성능 측정
- 이진 탐색은 처음 탐색을 시도할 때 탐색 대상의 범위가 1/2로 줄어듬
- 그 다음 시도에서는 원본 데이터의 1/4로 줄어듬
- 여기서 또 한 번 탐색을 시도하면 1/16로 탐색 대상의 범위가 줄어듬
- 이런 식으로 탐색 대상의 범위가 계속 줄어들어 마침내 '1'이 되면 탐색을 종료
최대 탐색 반복 횟수
- 데이터 크기 n, 탐색 반복 횟수 x, 탐색 완료 시점에 데이터 범위의 크기 1은 n에 1/2의 x 제곱을 곱한 값과 같음

- 이진 탐색의 최대 반복 횟수는 log2n
-> 데이터의 크기가 아무리 커져도 탐색 소요 시간은 아주 미미하게 증가
5.3.2 이진 탐색의 구현
이진 탐색 함수 BinarySearch
- 첫번째 매개변수 데이터(배열)
- 두번째 매개변수 데이터 크기
- 마지막 매개변수 찾고자 하는 목표값
ElementType BinarySearch(Score ScoreList[], int Size, ElementType Target)
{
int Left, Right, Mid;
Left = 0;
Right = Size -1;
//탐색 범위의 크기가 0이 될 떄까지 while문을 반복
while(Left<=Right)
{
Mid = (Left+Right) /2; //중앙 요소의 위치 계산
//중앙 요소가 담고 있는 값과 목표값이 일치하면 해당 요소를 반환
if(Target == ScoreList[Mid].socore)
return &(ScoreList[Mid]);
//목표값이 중앙요소보다 크면 범위를 오른편에 대해 이진 탐색 수행
else if (Target > ScoreList[Mid].score)
Left= Mid +1;
else
Right = Mid -1;
}
return NULL;
}'C언어 > 알고리즘' 카테고리의 다른 글
| [알고리즘] ch 5. 탐색(3) - 레드 블랙 트리 (2) | 2023.10.11 |
|---|---|
| [알고리즘] ch 5. 탐색(2) - 이진 탐색 트리 (0) | 2023.09.22 |
| [자료구조] ch 4. 트리 (2) - 수식 트리, 분리 집합 (0) | 2023.09.19 |
| [자료구조] ch 4 트리 (1) - 이진 트리 (2) | 2023.09.18 |
| [자료구조] ch 3. 큐 (0) | 2023.09.18 |



