5.5 레드 블랙 트리
레드 블랙 트리 (Red Black Tree)
- 레드 블랙 트리에서 노드의 색은 트리 전체의 균형을 유지할 수 있게 함
레드 블랙 트리의 노드 구조체
typedef int ElementType;
typedef struct tagRBTNode
{
struct tagRBTNode* Parent;
struct tagRBTNode* Left;
struct tagRBTNode* Right;
//노드의 색을 나타내는 Color 필드로, RED 아니면 BLACK 값을 저장 가능
enum { RED, BLACK }Color;
ElementType Data;
}RBTNode;
6.5.1 레드 블랙 트리의 구현 규칙
1) 모든 노드는 빨간색이거나 검은색이다
2) 뿌리 노드는 검은색이다
3) 잎 노드는 검은색이다
4) 빨간색 노드의 자식은 모두 검은색이다. (빨간색 노드는 연속되어 등장 불가)
5) 뿌리 노드와 모든 잎 노드 사이에 있는 검은색 노드의 수는 모두 동일하다
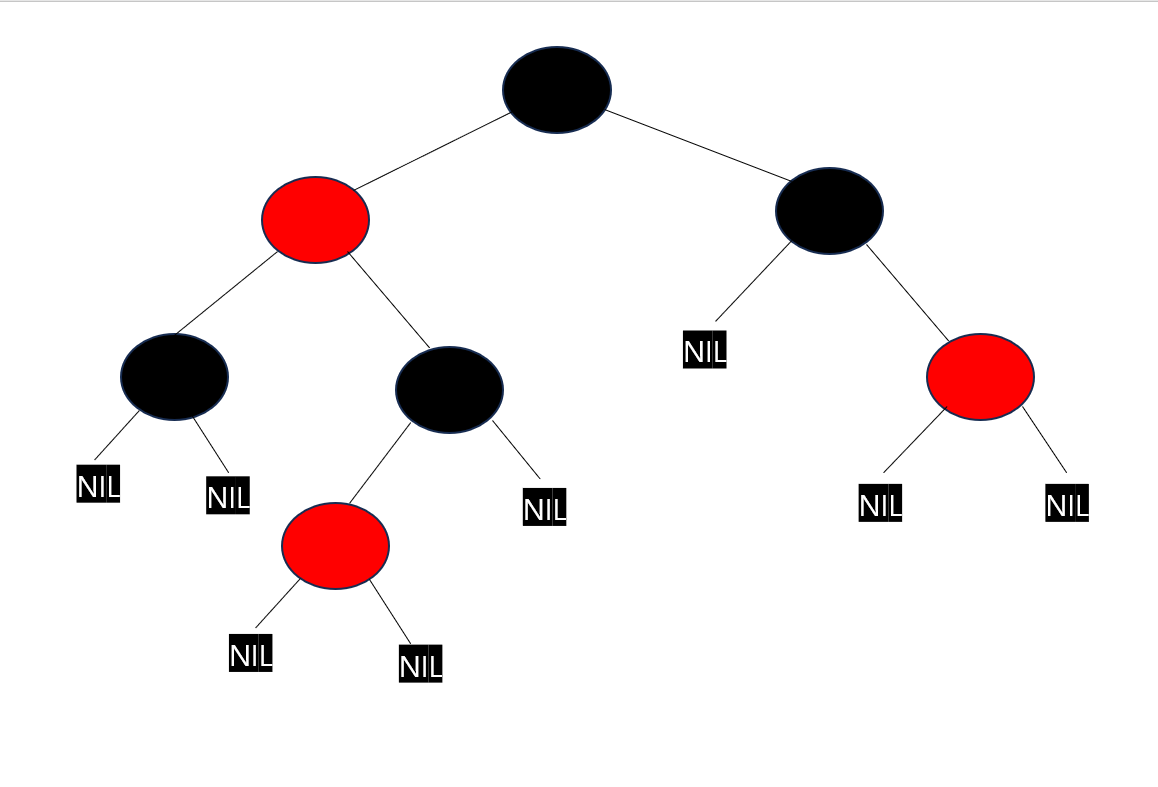
센티넬(Sentinel)노드
- NIL 노드는 아무 데이터도 갖고 있지 않지만 색깔만 검은색인 더미 노드
- 원래의 잎 노드들에 검은색이든 빨간색이든 NIL 노드를 양쪽 자식으로 연결하면 '모든 잎 노드는 검은색이다'라는 규칙 하나는 항상 지킬 수 있음
5.5.2 레드 블랙 트리의 기본 연산
1) 회전
- 회전(Rotate)는 부모와 자식 노드의 위치를 서로 바꾸는 연산
- 회전은 방향에 따라 우회전(Right-Rotate)와 좌회전(Left-Rotate)으로 나뉨
- 우회전 = 왼쪽 자식과 부모의 위치를 교환
- 좌회전 = 오른쪽 자식과 부모의 위치를 교환

- 이진 탐색 트리의 특성상 왼쪽 자식 노드는 부모 노드보다 작고 오른쪽 자식은 부모 보다 커야 함
- 단순히 부모와 자식 노드의 위치만 바꾸면 이진 탐색 트리의 조건이 무너짐
- 자식 노드 처리 필요
● 우회전할 때는 왼쪽 자식 노드의 오른쪽 자식 노드를 부모 노드의 왼쪽 자식 노드로 연결
root였던 8이 5로 변경되고 8은 5의 오른쪽 자식으로 들어가게 됨
이때 5의 오른쪽 자식 6이 8의 왼쪽 자식으로 옮겨짐
● 좌회전할 때는 오른쪽 자식 노드의 왼쪽 자식 노드를 부모 노드의 오른쪽 자식 노드로 연결
root였던 5가 8로 변경되고 5는 8의 왼쪽 자식으로 들어가게 됨
이때 8의 왼쪽 자식으로 6이 있었으므로 6은 떼어내서 5의 오른쪽 자식으로 옮겨짐
우회전 구현 함수 RBT_RotateRight
//우회전
void RBT_RotateRight(RBTNode** Root, RBTNode* Parent)
{
//왼쪽 자식의 오른쪽 자식 노드를 부모 노드의 왼쪽 자식으로 등록
RBTNode* LeftChild = Parent->Left;
Parent->Left = LeftChild->Right;
if (LeftChild->Right != Nil)
LeftChild->Right->Parent = Parent;
LeftChild->Parent = Parent->Parent;
//부모가 NULL이라면 이 노드는 Root
//이 경우에는 왼쪽 자식을 Root 노드로 만들어 회전
if (Parent->Parent == NULL)
(*Root) = LeftChild;
else
{
//왼쪽 자식 노드를 부모 노드가 있던 곳(할아버지의 자식 노드)에 위치
if (Parent == Parent->Parent->Left)
Parent->Parent->Left = LeftChild;
else
Parent->Parent->Right = LeftChild;
}
LeftChild->Right = Parent;
Parent->Parent = LeftChild;
}
좌회전 구현 함수 RBT_RotateLeft
//좌회전
void RBT_RotateLeft(RBTNode** Root, RBTNode* Parent)
{
//오른쪽 자식의 왼쪽 자식 노드를 부모 노드의 오른쪽 자식으로 등록
RBTNode* RightChild = Parent->Right;
Parent->Right = RightChild->Left;
if (RightChild->Left != Nil)
RightChild->Left->Parent = Parent;
RightChild->Parent = Parent->Parent;
//부모가 NULL이라면 이 노드는 Root 노드
//이 경우에는 오른쪽 자식을 Root 노드로 만들어 회전
if (Parent->Parent == NULL)
(*Root) = RightChild;
//오른쪽 자식 노드를 부모 노드가 있던 곳(할아버지의 자식 노드)에 위치시킴
else
{
if (Parent == Parent->Parent->Left)
Parent->Parent->Left = RightChild;
else
Parent->Parent->Right = RightChild;
}
RightChild->Left = Parent;
Parent->Parent = RightChild;
}
2) 노드 삽입 연산
- 레드 블랙 트리에 새 노드를 삽입하려면 이 노드를 빨간색으로 칠한 다음 NIL 노드를 이 노드의 양쪽 자식으로 연결해야 함
노드 삽입 함수 RBT_InsertNode
- 이진 탐색을 통해 새 노드를 트리에 삽입(RBT_InsertNodeHelper())
- 이 노드를 빨간색으로 칠하고 NIL 노드를 양쪽 자식으로 연결
- 앞서 수행된 작업 때문에 무너진 레드 블랙 트리의 규칙을 복구 (RBT_ResbuildAfterInsert())
//노드 삽입
void RBT_InsertNode(RBTNode** Tree, RBTNode* NewNode)
{
//이진 탐색 트리의 노드 삽입
RBT_InsertNodeHelper(Tree, NewNode);
//새 노드는 빨간색으로 칠하고 NIL을 양쪽 자식으로 연결
NewNode->Color = RED;
NewNode->Left = Nil;
NewNode->Right = Nil;
//무너진 레드 브랙 트리 규칙을 바로 잡음
RBT_RebuildAfterInsert(Tree, NewNode);
}
- 레드 블랙 트리 규칙 중 삽입으로 위반될 수 있는 규칙은 '뿌리 노드는 검은색이어야 한다' 와 '빨간색 노드의 자식들은 모두 검은색이다' 두가지
- '뿌리 노드는 검은색이어야 한다'
->뿌리 노드를 무조건 검은색으로 칠하면 해결
- '빨간색 노드의 자식들은 모두 검은색이다'
-> 삼촌 노드(부모노드의 형제노드)가 어떤 색인가에 따라 3가지 상황으로 나뉨
● 삼촌도 빨간색인 경우
● 삼촌이 검은색이며 새로 삽입한 노드가 부모 노드의 오른쪽 자식인 경우
● 삼촌이 검은색이며 새로 삽입한 노드가 부모 노드의 왼쪽 자식인 경우
삼촌도 빨간색인 경우
- 삼촌도 빨간색인 경우에는 부모 노드와 삼촌 노드를 검은색으로 칠하고 할아버지 노드를 빨간색으로 칠하면 됨

- 삼촌이 빨간색인 경우에 후속처리는 끝났지만 할아버지 노드를 빨간색으로 칠함으로써 4번 규칙이 또다시 위협받게 됨
-> 할아버지 노드를 새로 삽입한 노드로 간주하고 처음부터 4번 규칙을 위반하는 세가지 경우를 따져봐야 함
- 부모 노드가 검은색이거나 새로 삽입한 노드가 뿌리여야 비로소 이 굴레에 벗어날 수 있음
삼촌이 검은색이며 새로 삽입한 노드가 부모 노드의 오른쪽 자식인 경우
- 부모 노드를 좌회전(오른쪽 자식과 부모의 위치 교환)시켜 상황을 '삼촌이 검은색이며 새로 삽입한 부모 노드의 왼쪽자식인 경우'로 바꿈
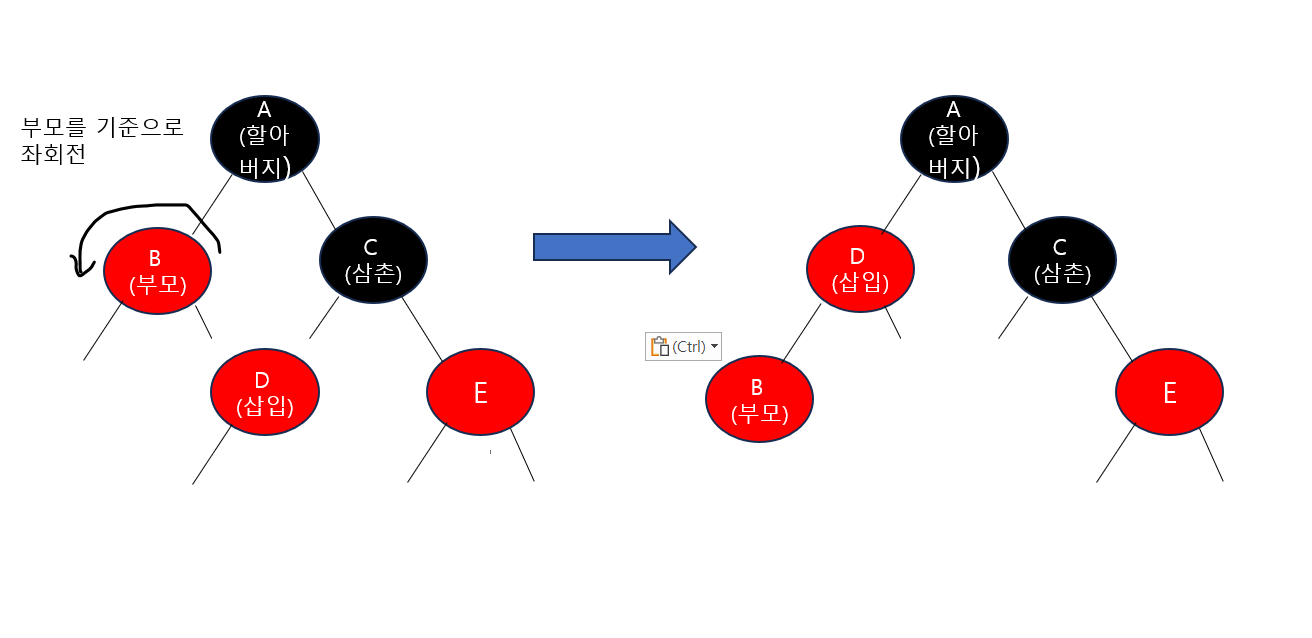
- 삽입한 노드 D가 부모가 되고 부모 노드였던 B가 자식이 됨
- 부모였던 노드를 삽입한 노드로 간주
삼촌이 검은색이며 새로 삽입한 노드가 부모 노드의 왼쪽 자식인 경우
- 부모 노드를 검은색, 할아버지 노드를 빨간색으로 칠한 다음 할아버지 노드를 우회전시킴

- 4번(빨간색 노드의 자식은 모두 검은색이다) 규칙이 위반되지 않음
- 새로 삽입한 노드 B의 부모 D가 검은색이기 때문
노드 삽입 후속처리 함수 RBT_RebuildAfterInsert
//노드 삽입 후속처리
void RBT_RebuildAfterInsert(RBTNode** Root, RBTNode* X)
{
//4번 규칙을 위반하는 동안에 계속 반복
while (X != (*Root) && X->Parent->Color == RED)
{
//부모 노드가 할아버지 노드의 왼쪽 자식인 경우
if (X->Parent == X->Parent->Parent->Left)
{
RBTNode* Uncle = X->Parent->Parent->Right;
//삼촌이 빨간색인 경우
if (Uncle->Color = RED)
{
//부모 노드와 삼촌 노드를 검은색으로
X->Parent->Color = BLACK;
Uncle->Color = BLACK;
//할아버지 노드를 빨간색으로
X->Parent->Parent->Color = RED;
//할아버지 노드를 새로 삽입한 노드로 간주
X = X->Parent->Parent;
}
else
{
//삼촌이 검은색이고 X가 오른쪽 자식인 경우
if (X == X->Parent->Right)
{
X = X->Parent;
//부모 노드를 좌회전
RBT_RotateLeft(Root, X);
}
//X가 왼쪽 자식인 경우
X->Parent->Color = BLACK; //부모 노드를 검은색으로
X->Parent->Parent->Color = RED; //할아버지 노드를 빨간색으로
RBT_RotateRight(Root, X->Parent->Parent); //할아버지 노드를 우회전
}
}
//부모가 할아버지 노드의 오른쪽 자식인 경우
else
{
RBTNode* Uncle = X->Parent->Parent->Left;
if (Uncle->Color == RED)
{
X->Parent->Color = BLACK;
Uncle->Color = BLACK;
X->Parent->Parent->Color = RED;
X = X->Parent->Parent;
}
else
{
if (X == X->Parent->Left)
{
X = X->Parent;
RBT_RotateRight(Root, X);
}
X->Parent->Color = BLACK;
X->Parent->Parent->Color = RED;
RBT_RotateLeft(Root, X->Parent->Parent);
}
}
}
(*Root)->Color = BLACK;
}
3) 노드 삭제 연산
- 빨간색 노드 삭제는 레드 블랙 트리의 규칙을 위반하지 않음
- 검은색 노드를 삭제하면 5번 규칙이 가장 먼저 무너짐
-> 삭제된 검은색 노드가 놓여 있던 뿌리 노드와 잎 노드 사이 경로의 검은색 노드 수가 다른 경로의 검은색 노드 수보다 하나 더 적어지기 때문
-> 삭제된 노드의 부모와 자식이 모두 빨간색이면 4번 규칙도 위반됨
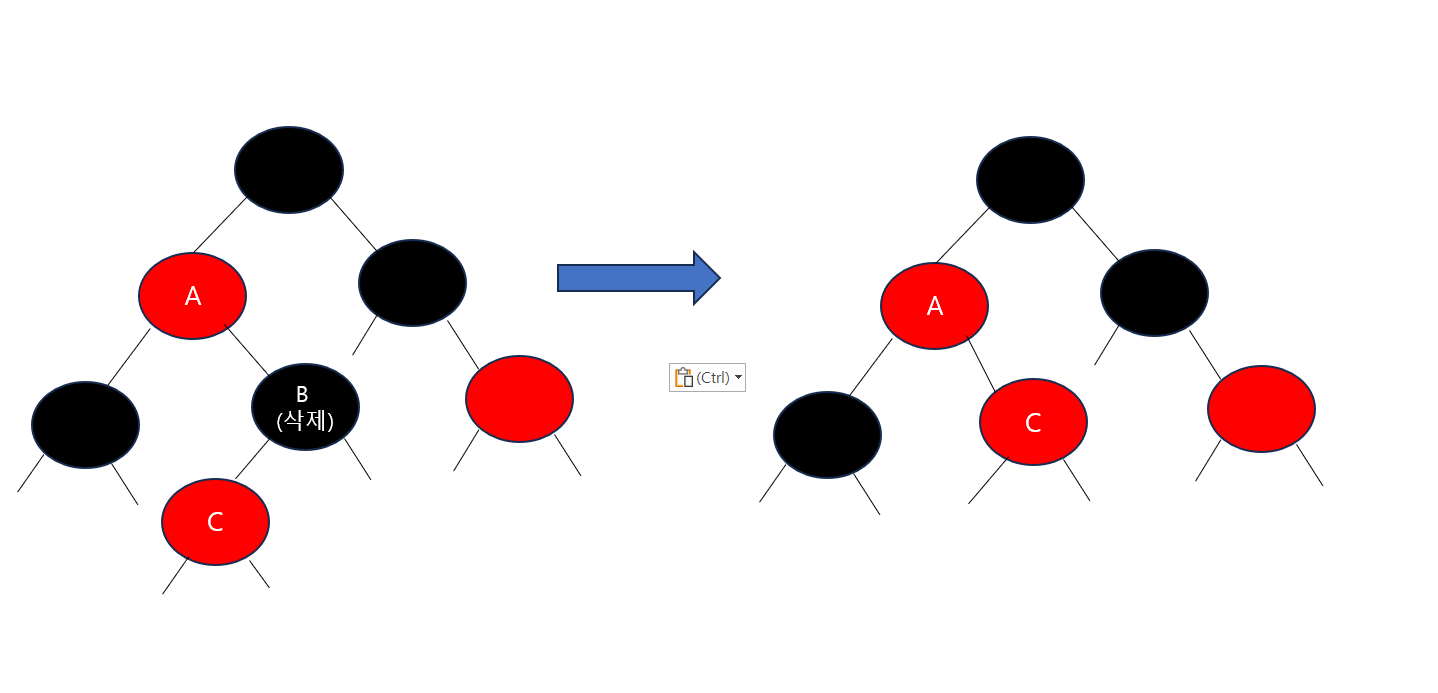
- 삭제된 노드를 대체하는 노드를 검은색으로 칠하면 4,5번 규칙을 보완 가능
- C 노드를 검은색으로 칠함으로써 4,5번 규칙을 모두 지켜냄

But, C 노드가 검은색이었다면 ?
- 4번 규칙은 위반 하지 않고, 모든 뿌리 노드와 잎 노드 사이 경로에 있는 검은색 노드 수가 동일해야 한다는 5번규칙만 위반
- 이 경우에도 대체 노드 C에 검은색을 덧입힘
- C 노드는 예외적으로 검은색을 '2개' 같게됨
- 이중 흑색 노드 = 검은색을 2개 갖는 노드

- 무너진 규칙은 1번(모든 노드는 빨간색이거나 검은색이다)으로 바뀜
- C 노드는 검은색도 빨간색도 아닌 '이중 흑색'이기 때문
- 이중 흑색 노드를 처리하는 방법
- 이중 노드의 형제와 조카들의 상태에 따라 4가지로 나뉨
● 형제가 빨간색인 경우
● 형제가 검은색이고
● - A 형제의 양쪽 자식이 모두 검은색인 경우
● - B 형제의 왼쪽 자식은 빨간색, 오른쪽 자식은 검은색인 경우
●- C 형제의 오른쪽 자식이 빨간색인 경우
형제가 빨간색인 경우
- 형제를 검은색, 부모를 빨간색으로 칠함
- 그 다음에는 부모를 기준으로 자식 노드를 좌회전
- 이렇게 하면 이중 흑색 노드는 그대로 남아 있지만 형제 노드는 검은색 노드로 바뀜
- 문제 유형이 '빨간색 형제'에서 '검은색 형제로' 변화
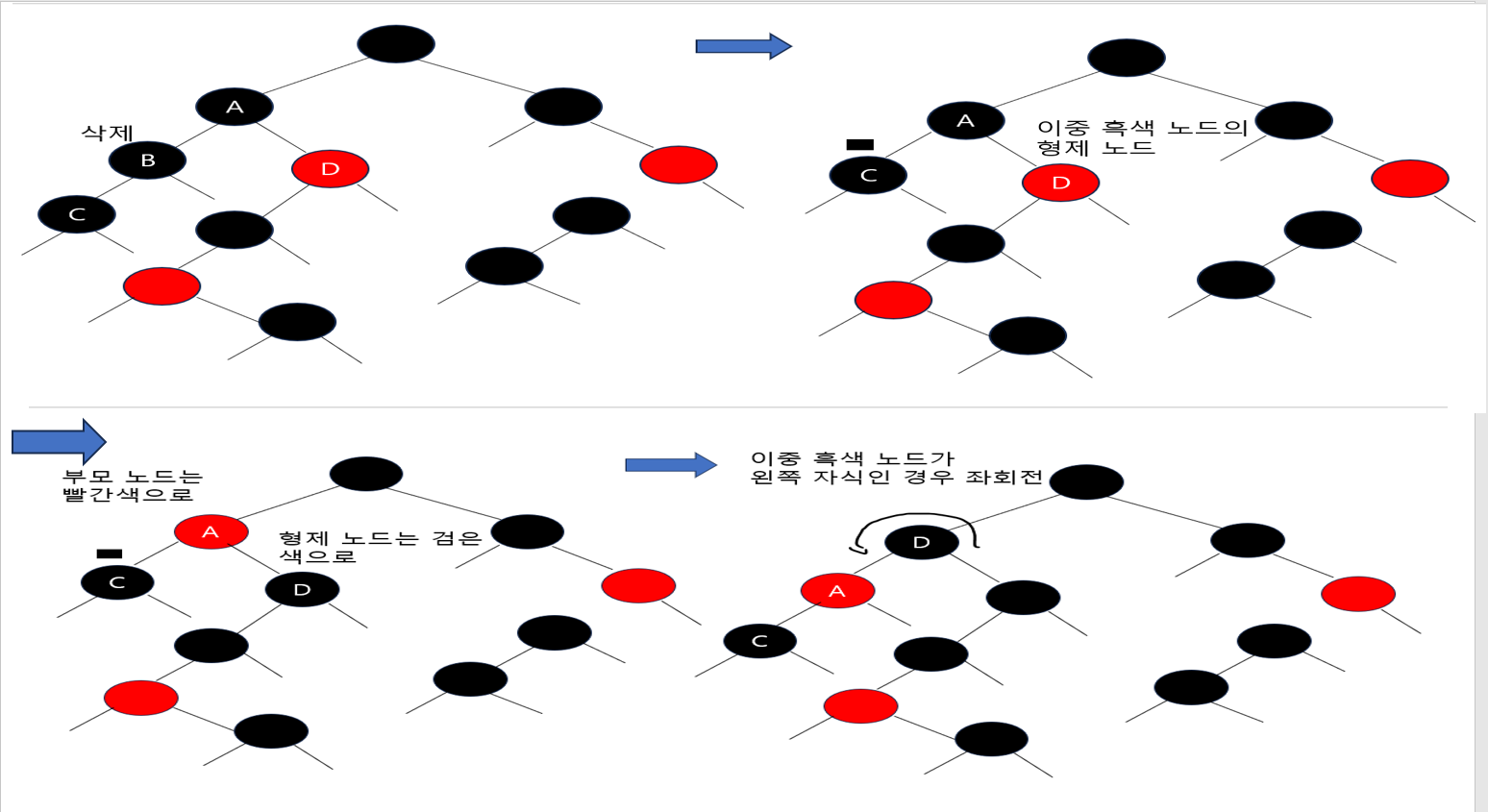
형제가 검은색이고, 형제의 양쪽 자식이 모두 검은색인 경우
- 형제 노드만 빨간색으로 칠한 후 이중 흑색 노드가 갖고 있던 검은색 중 하나를 부모 노드에게 넘겨줌
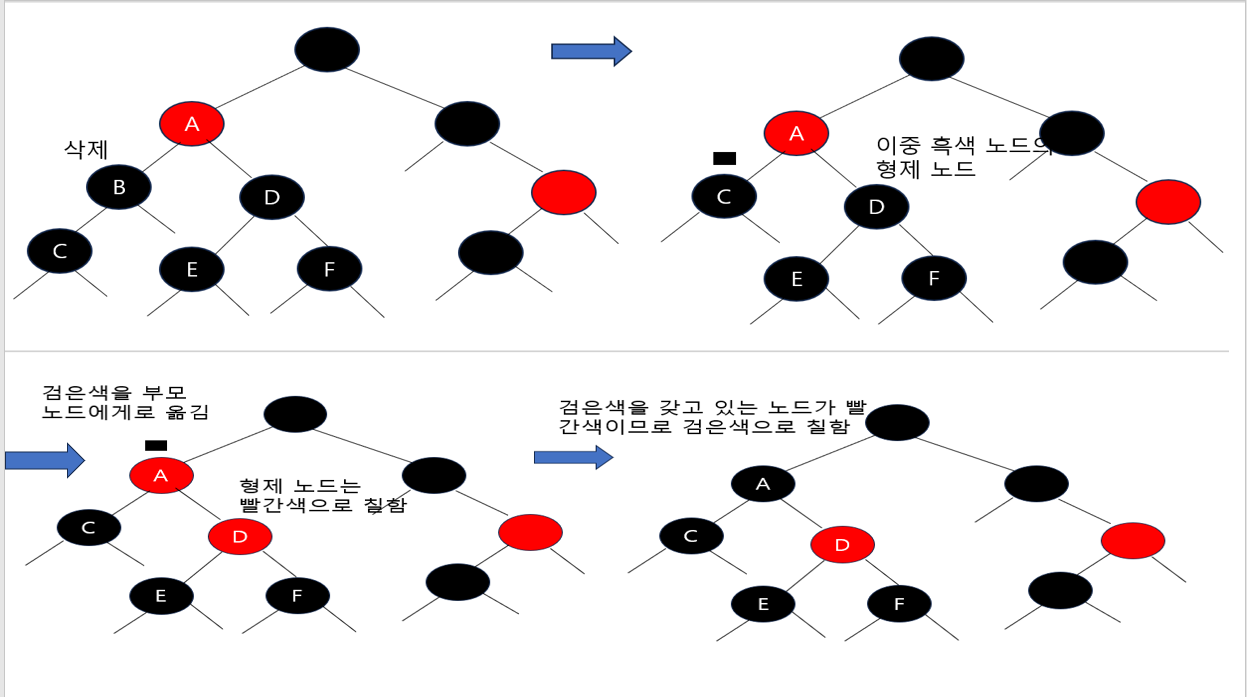
- 삭제된 B 노드를 대체하는 이중 흑색 노드 C는 형제 노드 D도 검은색이고 그 양쪽 자식인 E와 F도 모두 검은색
- D를 빨간색으로 칠하고 C가 갖고 있던 2개의 검은색 중 하나를 부모 노드인 A에게 넘김
- 부모 노드인 A는 자기가 넘겨받은 검은색을 적절하게 잘 처리하면 됨
형제가 검은색이고 형제의 왼쪽 자식은 빨간색, 오른쪽 자식은 검은색인 경우
- 형제 노드를 빨간색으로 칠하고 왼쪽 자식을 검은색으로 칠한 다음
- 형제 노드를 기준으로 우회전
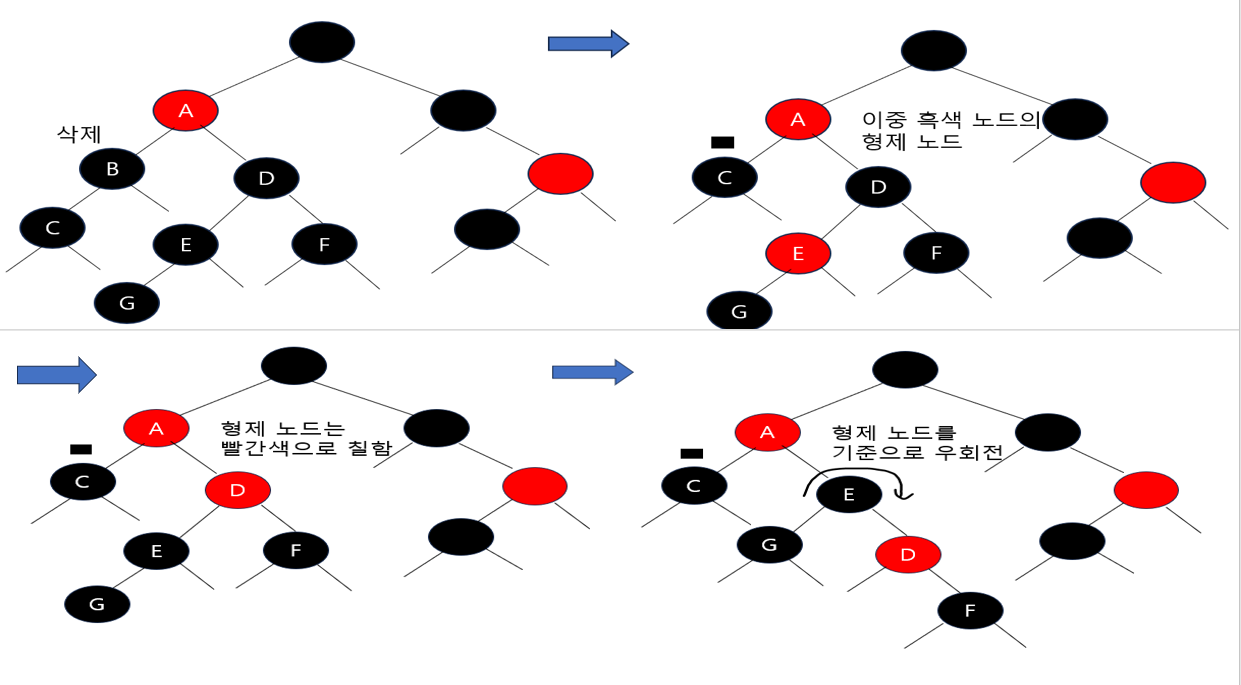
- B 노드를 삭제하면 C노드가 B노드를 대체하고 이중 흑색 노드로 변함
- 이중 흑색 노드의 형제 D가 검은색이고 형제의 왼쪽 자식인 E 노드는 빨간색, 오른쪽 자식인 F노드는 검은색
- 형제 노드 D를 빨간색, 형제 노드의 왼쪽 자식 노드 E를 검은색으로 칠함
- 그런 다음 형제 노드 D를 기준으로 우회전함으로써 뒤처리를 마무리
- 상황은 형제가 검은색이고 형제의 오른쪽 자식이 빨간색인 경우로 변화
형제가 검은색이고 형제의 오른쪽 자식이 빨간색인 경우
- 이중 흑색 노드의 부모가 갖고 있는 색을 형제 노드에 칠함
- 그 다음에 부모 노드와 형제 노드의 오른쪽 자식 노드를 검은색으로 칠하고 부모 노드를 기준으로 좌회전하면 1번 규칙이 지켜짐
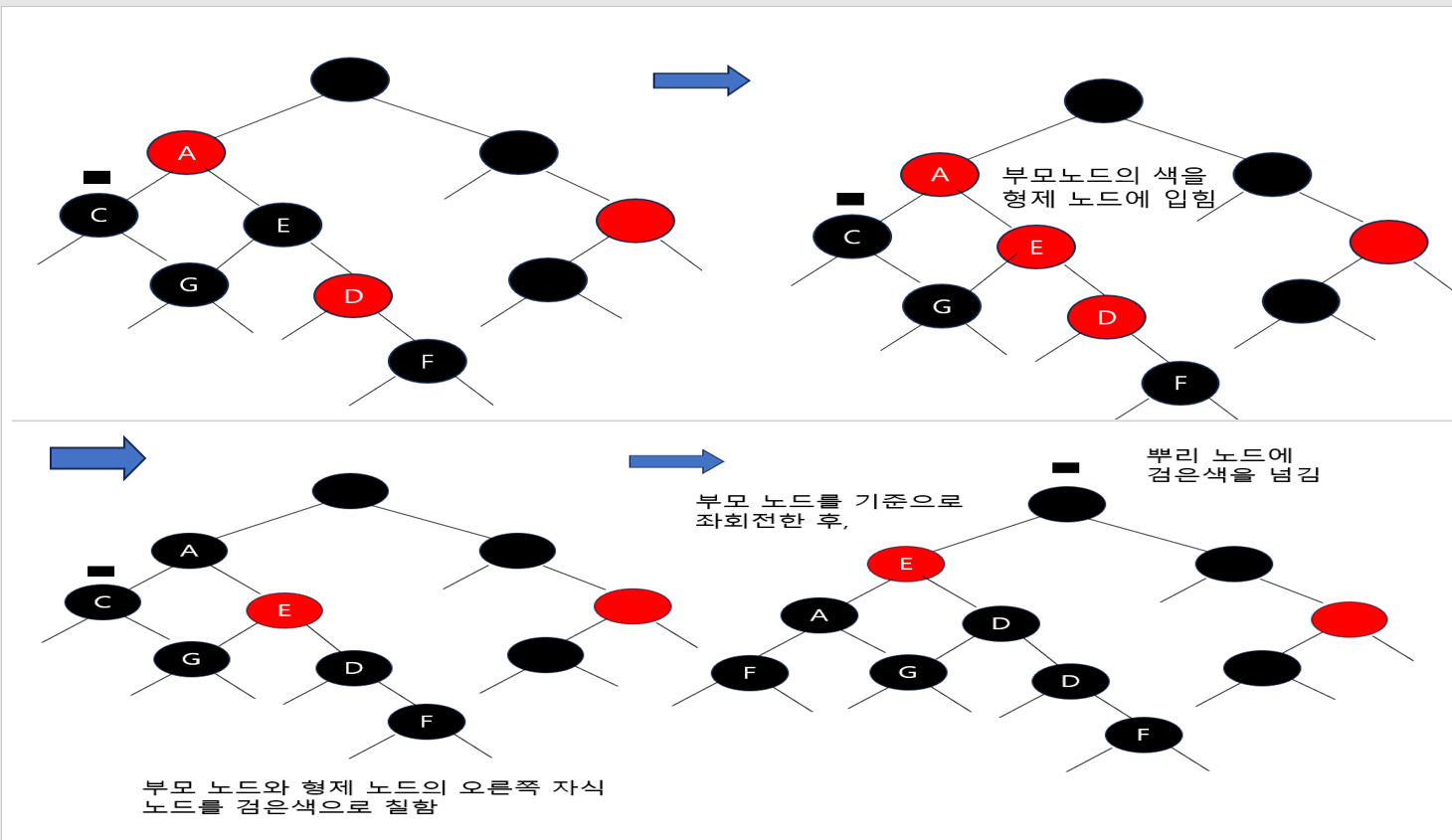
- C가 이중 흑색 노드였고 형제인 E 노드는 검은색, 형제의 오른쪽 자식 노드 D는 빨간색
- 부모 노드 A와 오른쪽 자식 노드인 D를 검은색으로 칠함
- 마지막으로 부모 노드 A를 기준으로 좌회전을 수행한 후 이중 흑색 노드 C가 갖고 있던 검은색 중 하나를 뿌리 노드에 넘김
- 뿌리 노드가 이중 흑색인 경우 검은색으로 칠해주기만 하면 상황이 끝남
노드 삭제 후속처리 함수 RBT_RebuildAfterRemove
//노드 삭제 후속처리
void RBT_RebuildAfterRemove(RBTNode** Root, RBTNode* Successor)
{
RBTNode* Sibling = NULL;
//뿌리 노드이거나 빨간색 노드로 검은색이 넘어가면 종료
while (Successor->Parent != NULL && Successor->Color == BLACK)
{
if (Successor == Successor->Parent->Left)
{
//이중 흑색 노드가 부모 노드의 왼쪽 자식인 경우
Sibling = Successor->Parent->Right;
//1) 형제가 빨간색인 경우
if (Sibling->Color == RED)
{
Sibling->Color = BLACK:
Successor->Parent->Color = RED;
RBT_RotateLeft(Root, Successor->Parent);
}
//형제가 검은색이며
else
{
//2)양쪽 자식이 모두 검은색인 경우
if (Sibling->Left->Color == BLACK && Sibling->Right->Color == BLACK)
{
Sibling->Color = RED;
Successor = Successor->Parent;
}
else
{
//3) 왼쪽 자식이 빨간색인 경우
if (Sibling->Left->Color == RED)
{
Sibling->Left->Color = BLACK:
Sibling->Color = RED;
RBT_RotateRight(Root, Sibling);
Sibling = Successor->Parent->Right;
}
//4) 오른쪽 자식이 빨간색인 경우
Sibling->Color = Successor->Parent->Color;
Successor->Parent->Color = BALCK;
Silbing->Right->Color = BLACK:
RBT_RotateLeft(Root, Successor->Parent);
Successor = (*Root);
}
}
}
else
{
//이중 흑색 노드가 부모 노드의 오른쪽 자식인 경우
Sibling = Successor->Parent->Left;
if (Sibling->Color == RED)
{
Sibling->Color = BLACK;
Successor->Parent->Color = RED;
RBT_RotateRight(Root, Successor->Parent);
}
else
{
if (Sibling->Right->Color == BLACK && Sibling->Left->Color == BLACK)
{
Sibling->Color = RED;
Successor = Successor->Parent;
}
else
{
if (Sibling->Right->Color == RED)
{
Sibling->Right->Color = BLACK;
Sibling->Color = RED;
RBT_RotateLeft(Root, Sibling);
Sibling = Successor->Parent->Left;
}
Sibling->Color = Successor->Parent->Color;
Successor->Parent->Color = BLACK;
Sibling->Left->Color = BLACK;
RBT_RotateRight(Root, Successor->Parent);
Successor = (*Root);
}
}
}
}
Successor->Color = BLACK:
}
5.5.3 레드 블랙 트리 예제 프로그램
RedBlackTree.c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef int ElementType;
extern RBTNode* Nil;
typedef struct tagRBTNode
{
struct tagRBTNode* Parent;
struct tagRBTNode* Left;
struct tagRBTNode* Right;
//노드의 색을 나타내는 Color 필드로, RED 아니면 BLACK 값을 저장 가능
enum { RED, BLACK }Color;
ElementType Data;
}RBTNode;
//노드 생성
RBTNode* RBT_CreateNode(ElementType NewData)
{
RBTNode* NewNode = (RBTNode*)malloc(sizeof(RBTNode));
NewNode->Parent = NULL;
NewNode->Left = NULL;
NewNode->Right = NULL;
NewNode->Data = NewData;
NewNode->Color = BLACK;
return NewNode;
}
//노드 제거
void RBT_DestroyNode(RBTNode* Node)
{
free(Node);
}
//트리 제거
void RBT_DestroyTree(RBTNode* Tree)
{
if (Tree->Right != Nil)
RBT_DestroyTree(Tree->Right);
if (Tree->Left != Nil)
RBT_DestroyTree(Tree->Left);
Tree->Left = Nil;
Tree->Right = Nil;
RBT_DestroyNode(Tree);
}
///노드 탐색
RBTNode* RBT_SearchNode(RBTNode* Tree, ElementType Target)
{
if (Tree == Nil)
return NULL;
if (Tree->Data > Target)
return RBT_SearchNode(Tree->Left, Target);
else if (Tree->Data < Target)
return RBT_SearchNode(Tree->Right, Target);
else
return Tree;
}
//최솟값 노드 탐색
RBTNode* RBT_SearchMinNode(RBTNode* Tree)
{
if (Tree == Nil)
return Nil;
if (Tree->Left == Nil)
return Tree;
else
return RBT_SearchMinNode(Tree->Left);
}
//노드 삽입
void RBT_InsertNode(RBTNode** Tree, RBTNode* NewNode)
{
//이진 탐색 트리의 노드 삽입
RBT_InsertNodeHelper(Tree, NewNode);
//새 노드는 빨간색으로 칠하고 NIL을 양쪽 자식으로 연결
NewNode->Color = RED;
NewNode->Left = Nil;
NewNode->Right = Nil;
//무너진 레드 브랙 트리 규칙을 바로 잡음
RBT_RebuildAfterInsert(Tree, NewNode);
}
//이진 탐색 트리의 노드 삽입
RBT_InsertNodeHelper(RBTNode** Tree, RBTNode* NewNode)
{
if ((*Tree) == NULL)
(*Tree) = NewNode;
if ((*Tree)->Data < NewNode->Data)
{
if ((*Tree)->Data < NewNode->Data)
{
if ((*Tree)->Right == Nil)
{
(*Tree)->Right = NewNode;
NewNode->Parent = (*Tree);
}
else
RBT_InsertNodeHelper(&(*Tree)->Right, NewNode);
}
else if ((*Tree)->Data > NewNode->Data)
{
if ((*Tree)->Left == Nil)
{
(*Tree)->Left = NewNode;
NewNode->Parent = (*Tree);
}
else
RBT_InsertNodeHelper(&(*Tree)->Left, NewNode);
}
}
}
//우회전
void RBT_RotateRight(RBTNode** Root, RBTNode* Parent)
{
//왼쪽 자식의 오른쪽 자식 노드를 부모 노드의 왼쪽 자식으로 등록
RBTNode* LeftChild = Parent->Left;
Parent->Left = LeftChild->Right;
if (LeftChild->Right != Nil)
LeftChild->Right->Parent = Parent;
LeftChild->Parent = Parent->Parent;
//부모가 NULL이라면 이 노드는 Root
//이 경우에는 왼쪽 자식을 Root 노드로 만들어 회전
if (Parent->Parent == NULL)
(*Root) = LeftChild;
else
{
//왼쪽 자식 노드를 부모 노드가 있던 곳(할아버지의 자식 노드)에 위치
if (Parent == Parent->Parent->Left)
Parent->Parent->Left = LeftChild;
else
Parent->Parent->Right = LeftChild;
}
LeftChild->Right = Parent;
Parent->Parent = LeftChild;
}
//좌회전
void RBT_RotateLeft(RBTNode** Root, RBTNode* Parent)
{
//오른쪽 자식의 왼쪽 자식 노드를 부모 노드의 오른쪽 자식으로 등록
RBTNode* RightChild = Parent->Right;
Parent->Right = RightChild->Left;
if (RightChild->Left != Nil)
RightChild->Left->Parent = Parent;
RightChild->Parent = Parent->Parent;
//부모가 NULL이라면 이 노드는 Root 노드
//이 경우에는 오른쪽 자식을 Root 노드로 만들어 회전
if (Parent->Parent == NULL)
(*Root) = RightChild;
//오른쪽 자식 노드를 부모 노드가 있던 곳(할아버지의 자식 노드)에 위치시킴
else
{
if (Parent == Parent->Parent->Left)
Parent->Parent->Left = RightChild;
else
Parent->Parent->Right = RightChild;
}
RightChild->Left = Parent;
Parent->Parent = RightChild;
}
//노드 삽입 후속처리
void RBT_RebuildAfterInsert(RBTNode** Root, RBTNode* X)
{
//4번 규칙을 위반하는 동안에 계속 반복
while (X != (*Root) && X->Parent->Color == RED)
{
//부모 노드가 할아버지 노드의 왼쪽 자식인 경우
if (X->Parent == X->Parent->Parent->Left)
{
RBTNode* Uncle = X->Parent->Parent->Right;
//삼촌이 빨간색인 경우
if (Uncle->Color = RED)
{
//부모 노드와 삼촌 노드를 검은색으로
X->Parent->Color = BLACK;
Uncle->Color = BLACK;
//할아버지 노드를 빨간색으로
X->Parent->Parent->Color = RED;
//할아버지 노드를 새로 삽입한 노드로 간주
X = X->Parent->Parent;
}
else
{
//삼촌이 검은색이고 X가 오른쪽 자식인 경우
if (X == X->Parent->Right)
{
X = X->Parent;
//부모 노드를 좌회전
RBT_RotateLeft(Root, X);
}
//X가 왼쪽 자식인 경우
X->Parent->Color = BLACK; //부모 노드를 검은색으로
X->Parent->Parent->Color = RED; //할아버지 노드를 빨간색으로
RBT_RotateRight(Root, X->Parent->Parent); //할아버지 노드를 우회전
}
}
//부모가 할아버지 노드의 오른쪽 자식인 경우
else
{
RBTNode* Uncle = X->Parent->Parent->Left;
if (Uncle->Color == RED)
{
X->Parent->Color = BLACK;
Uncle->Color = BLACK;
X->Parent->Parent->Color = RED;
X = X->Parent->Parent;
}
else
{
if (X == X->Parent->Left)
{
X = X->Parent;
RBT_RotateRight(Root, X);
}
X->Parent->Color = BLACK;
X->Parent->Parent->Color = RED;
RBT_RotateLeft(Root, X->Parent->Parent);
}
}
}
(*Root)->Color = BLACK;
}
//노드 삭제
RBTNode* RBT_RemoveNode(RBTNode** Root, ElementType Data)
{
RBTNode* Removed = NULL;
RBTNode* Successor = NULL;
RBTNode* Target = RBT_SearchNode((*Root), Data);
if (Target == NULL)
return NULL;
if (Target->Left == Nil || Target->Right == Nil)
{
Removed = Target;
}
else
{
Removed = RBT_SearchMinNode(Target->Right);
Target->Data = Removed->Data;
}
if (Removed->Left != Nil)
Successor = Removed->Left;
else
Successor = Removed->Right;
Successor->Parent = Removed->Parent;
if (Removed->Parent == NULL)
(*Root) = Successor;
else
{
if (Removed == Removed->Parent->Left)
Removed->Parent->Left = Successor;
else
Removed->Parent->Right = Successor;
}
if (Removed->Color == BLACK)
RBT_RebuildAfterRemove(Root, Successor);
return Removed;
}
//노드 삭제 후속처리
void RBT_RebuildAfterRemove(RBTNode** Root, RBTNode* Successor)
{
RBTNode* Sibling = NULL;
//뿌리 노드이거나 빨간색 노드로 검은색이 넘어가면 종료
while (Successor->Parent != NULL && Successor->Color == BLACK)
{
if (Successor == Successor->Parent->Left)
{
//이중 흑색 노드가 부모 노드의 왼쪽 자식인 경우
Sibling = Successor->Parent->Right;
//1) 형제가 빨간색인 경우
if (Sibling->Color == RED)
{
Sibling->Color = BLACK:
Successor->Parent->Color = RED;
RBT_RotateLeft(Root, Successor->Parent);
}
//형제가 검은색이며
else
{
//2)양쪽 자식이 모두 검은색인 경우
if (Sibling->Left->Color == BLACK && Sibling->Right->Color == BLACK)
{
Sibling->Color = RED;
Successor = Successor->Parent;
}
else
{
//3) 왼쪽 자식이 빨간색인 경우
if (Sibling->Left->Color == RED)
{
Sibling->Left->Color = BLACK:
Sibling->Color = RED;
RBT_RotateRight(Root, Sibling);
Sibling = Successor->Parent->Right;
}
//4) 오른쪽 자식이 빨간색인 경우
Sibling->Color = Successor->Parent->Color;
Successor->Parent->Color = BALCK;
Silbing->Right->Color = BLACK:
RBT_RotateLeft(Root, Successor->Parent);
Successor = (*Root);
}
}
}
else
{
//이중 흑색 노드가 부모 노드의 오른쪽 자식인 경우
Sibling = Successor->Parent->Left;
if (Sibling->Color == RED)
{
Sibling->Color = BLACK;
Successor->Parent->Color = RED;
RBT_RotateRight(Root, Successor->Parent);
}
else
{
if (Sibling->Right->Color == BLACK && Sibling->Left->Color == BLACK)
{
Sibling->Color = RED;
Successor = Successor->Parent;
}
else
{
if (Sibling->Right->Color == RED)
{
Sibling->Right->Color = BLACK;
Sibling->Color = RED;
RBT_RotateLeft(Root, Sibling);
Sibling = Successor->Parent->Left;
}
Sibling->Color = Successor->Parent->Color;
Successor->Parent->Color = BLACK;
Sibling->Left->Color = BLACK;
RBT_RotateRight(Root, Successor->Parent);
Successor = (*Root);
}
}
}
}
Successor->Color = BLACK:
}
//트리 출력
void RBT_PrintTree(RBTNode* Node, int Depth, int BlackCount)
{
int i = 0;
char c = 'X';
int v = -1;
char cnt[100];
if (Node == NULL || Node == Nil)
return;
if (Node->Color == BLACK)
BlackCount++;
if (Node->Parent != NULL)
{
v = Node->Parent->Data;
if (Node->Parent->Left == Node)
c = 'L';
else
c = 'R';
}
if (Node->Left == Nil && Node->Right == Nil)
sprint(cnt, " --------%d", BlackCount);
else
strncpy(cnt, "". sizeof(cnt));
for (i = 0; i < Depth; i++)
printf(" ");
printf("%d %s [%c, %d] %s\n", Node->Data,
(Node->Color == RED) ? "RED" : "BLACK", c, v, cnt);
RBT_PrintTree(Node->Left, Depth + 1, BlackCount);
RBT_PrintTree(Node->Right, Depth + 1, BlackCount);
}
'C언어 > 알고리즘' 카테고리의 다른 글
| [알고리즘] ch 7. 그래프 (1) (0) | 2023.10.25 |
|---|---|
| [알고리즘] ch 6 우선순위 큐와 힙 (1) | 2023.10.11 |
| [알고리즘] ch 5. 탐색(2) - 이진 탐색 트리 (0) | 2023.09.22 |
| [알고리즘] ch 5. 탐색 (1)- 순차 탐색, 이진 탐색 (0) | 2023.09.21 |
| [자료구조] ch 4. 트리 (2) - 수식 트리, 분리 집합 (0) | 2023.09.19 |



