7.1 그래프의 개요
- 그래프는 '정점의 모음'과 이 정점을 잇는 '간선의 모음'이 결합한 것
- 정점의 집합을 V, 간선의 집합을 E, 그래프를 G라고 했을 때 G=(V,E)이다.
- 간선으로 연결된 두 정점을 가리켜 서로 '인접(Adjacent)'또는 '이웃 관계'에 있다고 말함
- 간선을 통해 서로 이웃이 된 각 정점은 그래프 안에서 길을 만듬
ex) 정점 A에서 정점 C까지는 A,B,C가 하나의 경로(path)를 이루고, A,D,C가 또 하나의 경로를 형성함
- 경로는 길이를 가지는데, '길이'는 정점과 정점 사이에 있는 간선의 수로 정의
ex) 경로 A,B,C 사이에는 간선이 (A,B)와 (B,C) 2개가 있으니 길이가 2
- 사이클(Cycle) = 어느 경로가 정점 하나를 두번이상 거치도록 되어 있는 경로
- 방향성 그래프 (Directed Graph)
- 간선에 방향성이 있는 그래프
- 무방향성 그래프 (Directed Graph)
- 간선에 방향성이 없는 그래프
- 두 정점 사이에 경로가 존재하면 이 두 정점이 연결되어 있다고 함
7.2 그래프 표현 방법
- 그래프의 표현 문제는 '간선. 즉 정점과 정점의 인접 관계를 어떻게 나타내는가?'의 문제로 귀결
- 행렬을 이용하는 방법 = 인접 행렬(Adjacnecy Matrix)
- 리스트를 이용하는 방법 = 인접 리스트(Adjacnecy list)
7.2.1 인접 행렬
1) 인접 행렬(Adjacnecy Matrix)
- 정점끼리의 인접 관계를 나타내는 행렬
- 그래프의 정점 수를 N이라고 했을 떄 N*N 크기의 행렬을 만들어 한 정점과 또 다른 정점이 인접해 있는 경우 행렬의 각 원소를 1로 표시하고 인접해 있지 않은 경우 0으로 표시
ex) 방향성 그래프
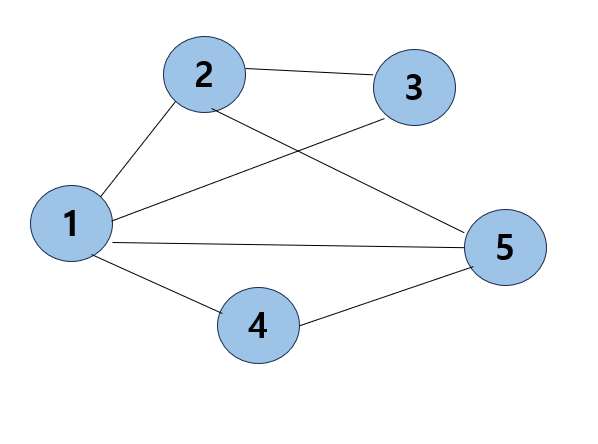
- 정점 1은 정점 2,3,4,5와 인접해 있으므로 (1,2), (1,3), (1,4), (1,5)는 모두 1
- 정점 1은 자기 자신과 인접관계를 만들 수 없으므로 (1,1)은 0
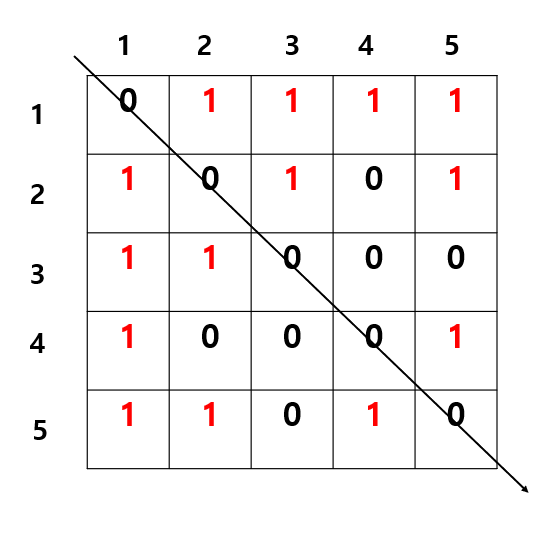
- (1,1),(2,2),(3,3),(4,4),(5,5)를 따라 선을 죽 그어서 행렬을 둘로 나누면
- 인접 행렬이 주 대각선을 기준으로 대칭(Symmetric)을 이룬다는 사실을 알 수 있음
- 무방향성의 그래프의 인접행렬은 이처럼 주 대각선을 기준으로 대칭을 이룸
ex) 방향성 그래프
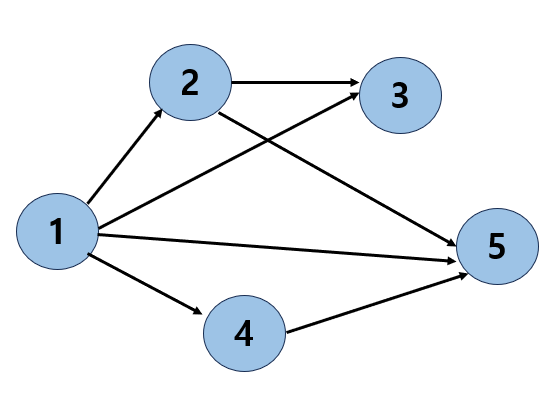
- 방향성 그래프에서의 정점은 자신이 직접 간선을 통해 가리키고 있는 정점에서만 인접해 있다고 표현
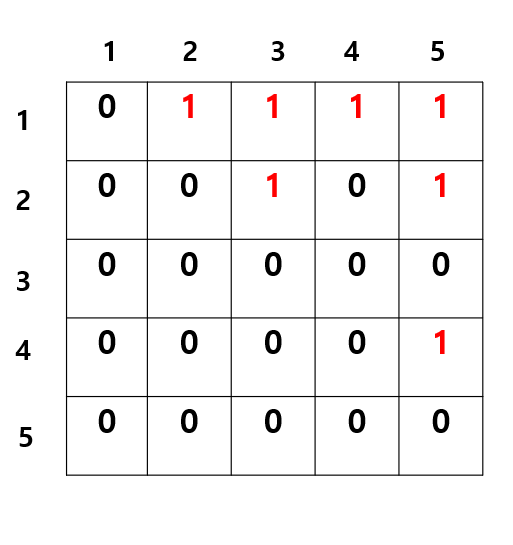
7.2.2 인접 리스트
1) 인접 리스트(Adjacency list)
- 그래프 내 각 정점의 인접 관계를 표현하는 리스트
- 각 정점이 자신과 인접한 모든 정점의 목록을 리스트로 관리하도록 하는 기법
- 모든 정점을 죽 늘어놓고 각 정점의 인접 정점을 옆에 나열
ex) 무방향성 그래프
| 정점 | 인접 정점 |
| 1 | 2,3,4,5 |
| 2 | 1,3,5 |
| 3 | 1,2 |
| 4 | 1,5 |
| 5 | 1,2,4 |
ex) 방향성 그래프
| 정점 | 인접 정점 |
| 1 | 2,3,4,5 |
| 2 | 3,5 |
| 3 | |
| 4 | 5 |
| 5 |
2) 인접 행렬과 인접 리스트 비교
| 장점 | 단접 | |
| 인접 행렬 | - 정점 간의 인접 여부를 빠르게 알 수 있음 | - 인접 관계를 행렬 형태로 저장하기 위해 사용하는 메모리의 양이 '정점의 크기 *N^2만큼 커짐 |
| 인접 리스트 | - 정점과 간선의 삽입이 빠르고 인접 관계를 표시하는 리스트에 사용되는 메모리의 양이 적음 | - 정점 간의 인접 여부를 알아내기 위해 인접 리스트를 타고 순차탐색을 해야 함 |
3) 인접 리스트의 구현
정점 구조체
//정점 구조체
typedef struct tagVertex
{
VElementType Data;
int Visited;
int Index;
struct tagVertex* Next;
struct tagEdge* AdjacencyList;
}Vertex;- Data = 데이터를 담는 필드
- Next = 다음 정점을 가리키는 포인터
- Adjacency LIst = 인접 정점의 목록에 대한 포이넡
- Visited = 방문 여부, 그래프 순환 알고리즘에서 사용할 필드
- Index = 정점의 인덱스, 최단 경로 탐색 알고리즘에서 사용할 필드
간선 구조체
//간선 구조체
typedef struct tagEdge
{
int Weight;
struct tagEdge* Next;
Vertex* From;
Vertex* Target;
}Edge;- From = 간선의 시작 정점
- Target = 간선의 끝 정점
- Next = 다음 간선을 가리키는 포인터
- Weight = 간선의 가중치,
최소 신장 트리나 최단 경로 탐색 알고리즘에서 정점 사이의 거리나 비용 등을 표현하기 위해 사용
그래프 구조체
//그래프 구조체
typedef struct tagGraph
{
Vertex* Vertices;
int VertexCount;
}Graph;- Vertices = 정점 목록에 대한 포인터
- Vertex Count = 정점 수
인접 리스트 예제 프로그램
#include <stdio.h>
#include <stdlib.h>
enum VisitMode {Visited, NotVisited};
typedef int VElementType;
//정점 구조체
typedef struct tagVertex
{
VElementType Data;
int Visited;
int Index;
struct tagVertex* Next;
struct tagEdge* AdjacencyList;
}Vertex;
//간선 구조체
typedef struct tagEdge
{
int Weight;
struct tagEdge* Next;
Vertex* From;
Vertex* Target;
}Edge;
//그래프 구조체
typedef struct tagGraph
{
Vertex* Vertices;
int VertexCount;
}Graph;
//그래프 생성
Graph* CreateGraph()
{
Graph* graph = (Graph*)malloc(sizeof(Graph));
graph->Vertices = NULL;
graph->VertexCount = 0;
return graph;
}
//정점 생성
Vertex* CreateVertex(VElementType Data)
{
Vertex* V = (Vertex*)malloc(sizeof(Vertex));
V->Data = Data;
V->Next = NULL;
V->AdjacencyList = NULL;
V->Visited = NotVisited;
V->Index = -1;
return V;
}
//간선 생성
Edge* CreateEdge(Vertex* From, Vertex* Target, int Weight)
{
Edge* E = (Edge*)malloc(sizeof(Edge));
E->From = From;
E->Target = Target;
E->Next = NULL;
E->Weight = Weight;
return E;
}
//정점 추가
void AddVertex(Graph* G, Vertex* V)
{
Vertex* VertexList = G->Vertices;
if (VertexList == NULL)
{
G->Vertices = V;
}
else
{
while (VertexList->Next != NULL)
VertexList = VertexList->Next;
VertexList = G->VertexCount++;
}
}
//간선 추가
void AddEdge(Vertex* V, Edge* E)
{
if (V->AdjacencyList == NULL)
{
V->AdjacencyList = E;
}
else
{
Edge* AdjacencyList = V->AdjacencyList;
while (AdjacencyList->Next != NULL)
AdjacencyList = AdjacencyList->Next;
AdjacencyList->Next = E;
}
}
//간선 파괴
void DestroyEdge(Edge* E)
{
free(E);
}
//정점 파괴
void DestroyVertex(Vertex* V)
{
while (V->AdjacencyList != NULL)
{
Edge* Edge = V->AdjacencyList->Next;
DestroyEdge(V->AdjacencyList);
V->AdjacencyList = Edge;
}
free(V);
}
//그래프 파괴
void DestroyGraph(Graph* G)
{
while (G->Vertices != NULL)
{
Vertex* Vertices = G->Vertices->Next;
G->Vertices = Vertices;
}
free(G);
}
//그래프 출력
void PrintGraph(Graph* G)
{
Vertex* V = NULL;
Edge* E = NULL;
if ((V = G->Vertices) == NULL)
return;
while (V != NULL)
{
printf("%c :", V->Data);
if ((E = V->AdjacencyList) == NULL) {
V = V->Next;
printf("\n");
continue;
}
while (E != NULL)
{
printf("%c[%d]", E->Target->Data, E->Weight);
E = E->Next;
}
printf("\n");
V = V->Next;
}
printf("\n");
}
int main(void)
{
//그래프 생성
Graph* G = CreateGraph();
//정점 생성
Vertex* V1 = CreateVertex('1');
Vertex* V2 = CreateVertex('2');
Vertex* V3 = CreateVertex('3');
Vertex* V4 = CreateVertex('4');
Vertex* V5 = CreateVertex('5');
//그래프에 정점을 추가
AddVertex(G, V1);
AddVertex(G, V2);
AddVertex(G, V3);
AddVertex(G, V4);
AddVertex(G, V5);
//정점과 정점을 간선으로 잇기
AddEdge(V1, CreateEdge(V1, V2, 0));
AddEdge(V1, CreateEdge(V1, V3, 0));
AddEdge(V1, CreateEdge(V1, V4, 0));
AddEdge(V1, CreateEdge(V1, V5, 0));
AddEdge(V2, CreateEdge(V2, V1, 0));
AddEdge(V2, CreateEdge(V2, V3, 0));
AddEdge(V2, CreateEdge(V2, V5, 0));
AddEdge(V3, CreateEdge(V3, V1, 0));
AddEdge(V3, CreateEdge(V3, V2, 0));
AddEdge(V4, CreateEdge(V4, V1, 0));
AddEdge(V4, CreateEdge(V4, V5, 0));
AddEdge(V5, CreateEdge(V5, V1, 0));
AddEdge(V5, CreateEdge(V5, V2, 0));
AddEdge(V5, CreateEdge(V5, V4, 0));
PrintGraph(G);
//그래프 소멸
DestroyGraph(G);
return 0;
}
7.3 그래프 순회 기법
순환 알고리즘(Traversal Algorithm)
- 그래프의 정점을 모두 한번씩 방문하는 알고리즘
- 순환 알고리즘의 두가지 종류
1) 너비 우선 탐색은 그래프에서 최단 경로를 찾는 알고리즘의 기반이 됨
2) 깊이 우선 탐색은 그래프 정렬 알고리즘의 기반이 됨
7.3.1 깊이 우선 탐색
깊이 우선 탐색(Depth First Search)
- '더 나아갈 길이 보이지 않을 때까지 깊이 들어간다'
- 길이 나오지 않을 때까지 그래프의 정점을 타고 깊이 들어가다가 더 이상 방문해왔던 정점말고는 다른 이웃을 갖고 있지 않은 정점을 만나면 뒤로 돌아가 다른 경로로 뻗어 있는 정점을 타고 방문을 재개하는 방식으로 동작
DFS 동작 방식
1) 시작 정점을 밟은 후 이 정점을 "방문했음"으로 표시
2) 그리고 이 정점과 이웃 정점(인접 정점) 중에 아직 방문하지 않은 곳을 선택하여 이를 시작 정점으로 삼고 다시 깊이 우선 탐색을 시작.
3) 더 이상 방문하지 않은 이웃 정점이 없으면 이전 정점으로 돌아가 2)를 수행
4) 이전 정점으로 돌아가도 더 이상 방문할 이웃 정점이 없다면 그래프의 모든 정점을 방문했다는 뜻이므로 탐색을 종료
ex)
- 시작 정점을 밟은 후 이 정점을 '방문했음'으로 표시
- 1의 인접 정점 중 정점 2를 먼저 방문하고 '방문했음'을 표시
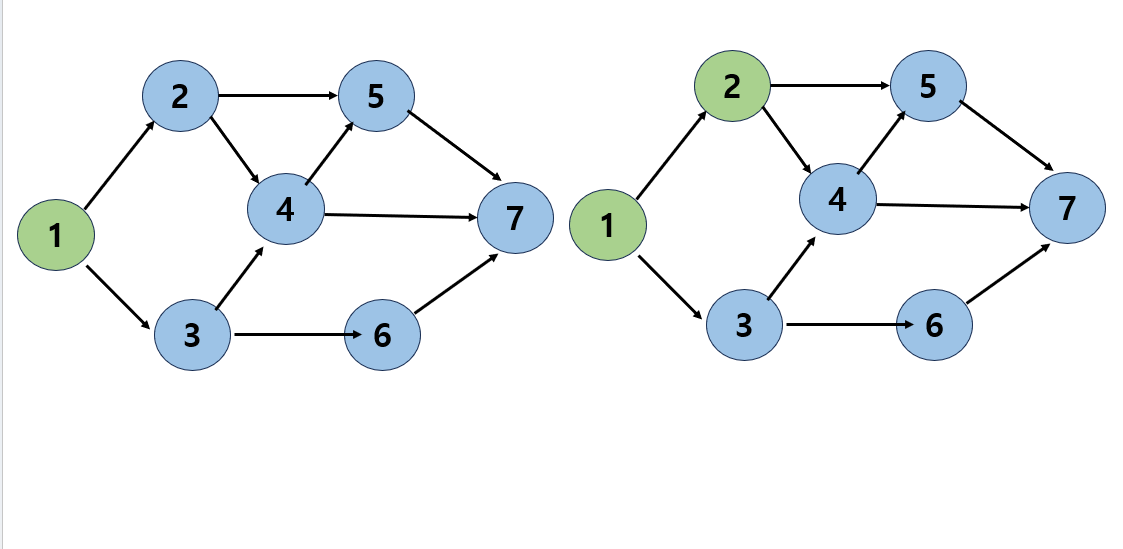
- 정점 2의 인접 정점중 정점 4를 방문하고 '방문했음'을 표시
- 정점 4의 인접 정점중 정점 5를 방문하고 7을 방문
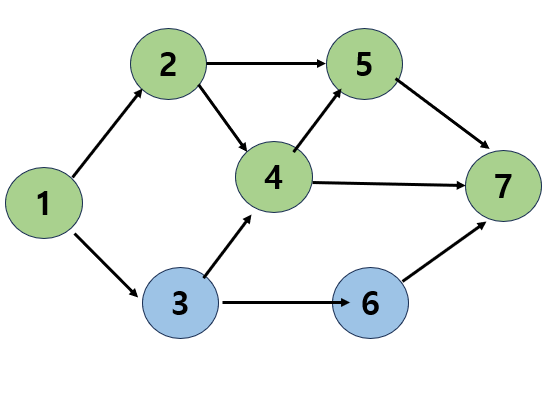
- 정점 7은 더 이상 방문할 인접 정점이 없으므로 정점 5로 돌아가서 방문하지 않은 인접 정점이 있는지 찾아보고
없다면 정점 4, 정점 2로 돌아가서 찾아봐야 함
- 정점 2마저도 방문하지 않은 이웃정점이 없으므로 정점 1로 되돌아감
- 정점 1에는 방문하지 않은 정점 3이 있음. 이 정점을 방문
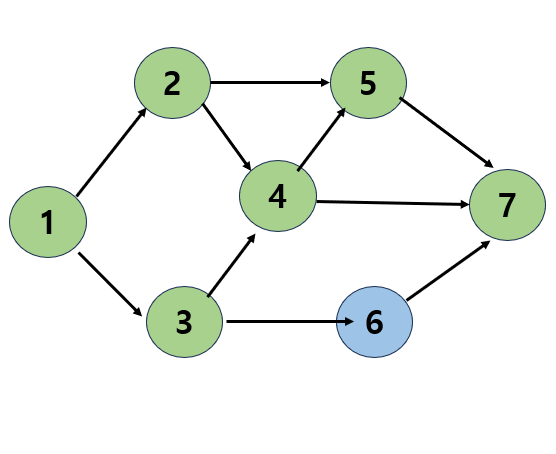
- 정점 3에는 인접 정점 4와 6이 있지만 4는 이미 방문한 적이 있으므로 6을 방문
- 정점 6에는 새로 방문할 정점이 없으므로 다시 뒤로 돌아가 방문할 곳을 찾아야 함
- 정점 3, 정점 1로 돌아가도 새로 방문할 곳이 없으니 탐색 종료
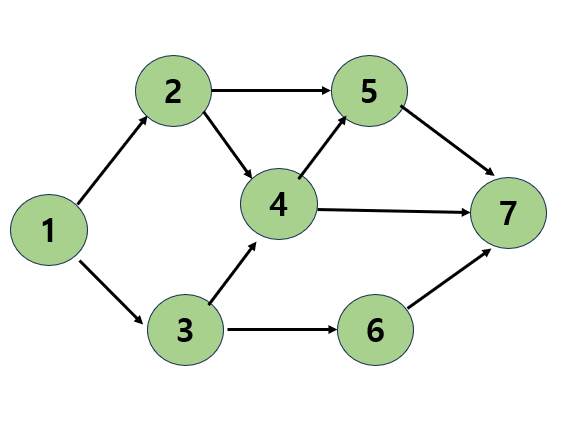
DFS() 함수
void DFS(Vertex* V)
{
Edge* E = NULL;
printf("%d", V->Data);
//방문한 정점에 "방문했음"이라고 표시
V->Visited = Visited;
E= V->AdjacencyList;
//현재 정점의 모든 인접 정점에 대해 DFS()를 재귀 호출
while(E!=NULL)
{
if(E->Target!=NULL && E->Target->Visited == NotVisited)
DFS(E->Target);
E = E->Next;
}
}
7.3.2 너비 우선 탐색
너비 우선 탐색(Breadth First Search)
- '꼼꼼하게 좌우를 살피며 다니자'
- 시작 정점을 지난 후 깊이가 1인 모든 정점을 방문하고 그다음에는 깊이가 2인 모든 정점을 방문
- 이런 식으로 한 단계씩 깊이를 더해가며 해당 깊이에 있는 모든 정점을 방문하다가 더 이상 방문할 정점이 없을 때 탐색을 종료
BFS 동작 방식
1) 시작 정점을 '방문했음'으로 표시하고 큐에 삽입
2) 큐로부터 정점을 제거. 제거한 정점의 인접 정점 중에서 아직 방문하지 않은 곳을 '방문했음'으로 표시하고 큐에 삽입
3) 큐가 비면 탐색이 끝난 것. 따라서 큐가 빌 떄까지 단계 2) 의 과정을 반복
ex)
- 시작 정점을 '방문했음'으로 표시하고 큐에 삽입
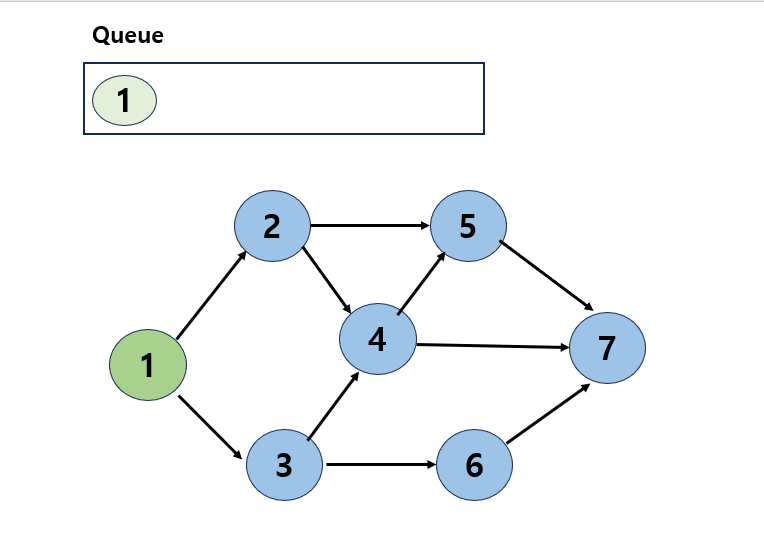
- 현재 큐에는 시작 정점 1이 있는데, 이를 큐에서 제거한 다음 인접 정점이 있는지 살핌.
- 1에는 아직 방문하지 않은 정점 2와 3이 있으므로 이 두 정점을 방문
- 방문한 정점은 큐에 삽입
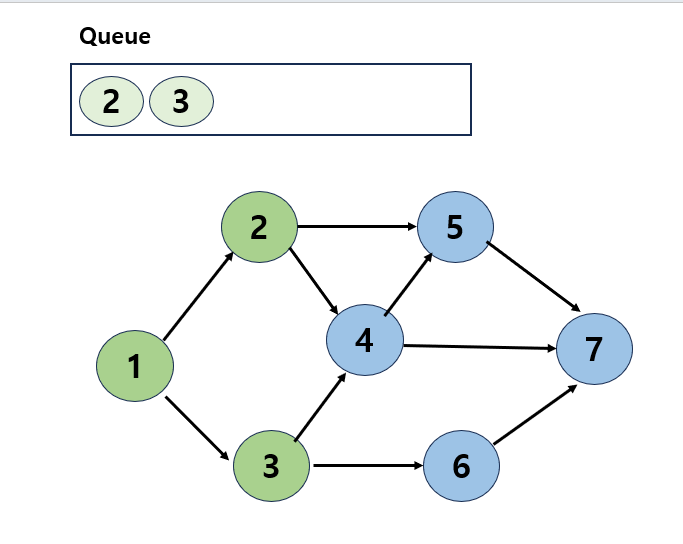
- 큐에는 2개의 정점이 들어 있는데 큐의 전단에 있는 정점을 제거한 후 이 정점의 인접 정점을 조사
- 정점 2에는 아직 방문하지 않은 정점 4,5가 인접해 있음
- 이들을 방문한 후 큐에 삽입
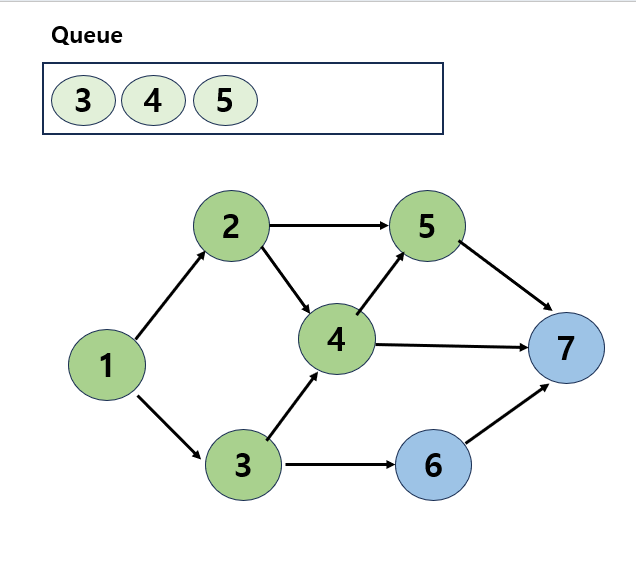
- 큐의 전단에 있는 3을 큐에서 제거하고 이 정점의 인접 정점을 조사
- 3에 인접한 정점 중 4는 이미 방문했고 6은 방문하지 않았으므로 6을 방문하고 큐에 삽입
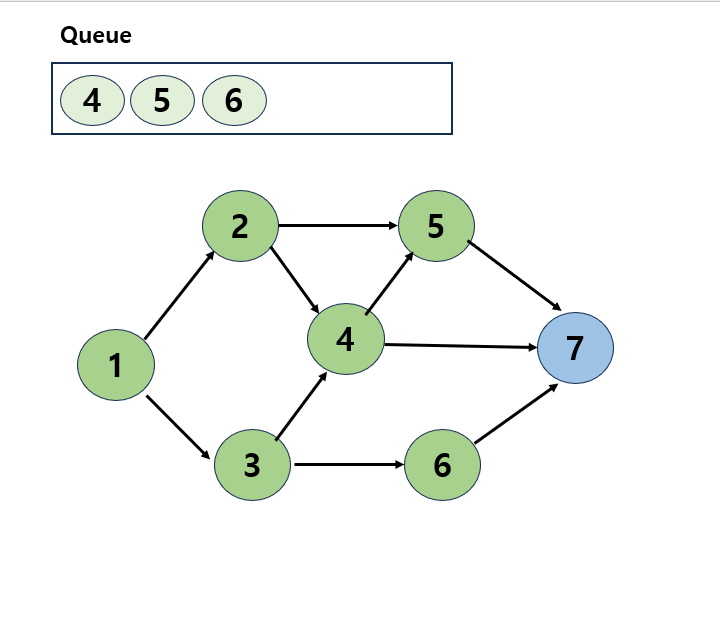
- 정점 4를 큐에서 제거하고 인접 정점을 찾음
- 정점 4에 인접한 정점은 5와 7뿐인데, 5는 이미 방문한 정점이므로 7을 방문한 후 큐에 삽입
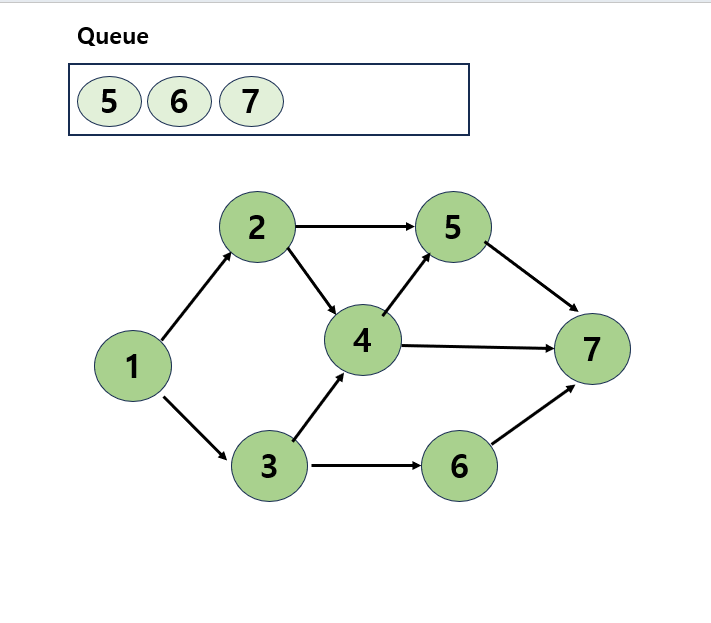
- 큐에 아직 5,6,7이 남아 있는데, 정점 5를 제거해도 남은 미방문 인접 정점이 없고 6을 제거해도 마찬가지.
정점 7은 아예 인접정점이 없음
- 큐에 남은 정점이 없으므로 탐색을 종료
- 정점 방문 순서
1->2->3->4->5->6
깊이 0 (정점 1) , 깊이 1(정점 2,3) , 깊이 2(정점 4,5,6) , 깊이 3( 정점 7)
BFS() 함수
void BFS(Vertex* V, LinkedQueue* Queue)
{
Edge * E = NULL;
printf("%d", V->Data);
V->Visited = Visited;
//시작 정점을 큐에 삽입
LQ_Enqueue(Queue, LQ_CreateNode(V));
//큐가 비어있는지 검사
while(!LQ_IsEmpty(Queue))
{
//큐에서 전단을 제거
Node* Popped = LQ_Dequeue(Queue);
V = Popped->Data;
E = V->AdjacencyList;
//큐에서 꺼낸 정점의 인접 정점을 조사
while(E!=NULL)
{
V=E->Target;
//미방문 정점만 방문
if(V!=NULL && V->Visited == NotVisited)
{
printf("%d ", V->Data);
V->Visited = Visited;
LQ_Enqueue(Queue, LQ_CreateNode(V));
}
E=E->Next;
}
}
}
'C언어 > 알고리즘' 카테고리의 다른 글
| [알고리즘] ch 7. 그래프 (3) - 최소 신장 트리(프림 알고리즘) (0) | 2023.11.06 |
|---|---|
| [알고리즘] ch 7. 그래프 (2) - 위상 정렬 (0) | 2023.10.25 |
| [알고리즘] ch 6 우선순위 큐와 힙 (1) | 2023.10.11 |
| [알고리즘] ch 5. 탐색(3) - 레드 블랙 트리 (2) | 2023.10.11 |
| [알고리즘] ch 5. 탐색(2) - 이진 탐색 트리 (0) | 2023.09.22 |



