6.1 우선순위 큐
우선순위 큐(Priority Queue)
- 우선순위 속성을 갖는 데이터의 삽입(Enqueue)과 제거(Dequeue)연산을 지원하는 ADT
- 큐는 먼저 들어온 요소가 무조건 먼저 나오게 하지만, 우선순위 큐는 새로운 요소에 우선순위를 부여해서 큐에 삽입하고 가장 높은 우선순위를 가진 요소부터 빠져나오게 함
6.1.1 우선순위 큐의 삽입/제거 연산
- 우선순위 큐의 각 요소는 '우선순위'를 가짐
1) 노드 삽입 연산
ex) 우선순위가 20인 요소 삽입
- 우선순위 큐의 첫 요소부터 순차적으로 우선순위를 비교

- 20은 2와 17보다 크고 22보다 작으므로 17과 22사이에 삽입
2) 노드 제거 연산
- 전단만 제거해서 반환

6.2 힙
힙(Heap)
- 힙 순서 속성(Heap Order Property)을 만족하는 완전 이진 트리
- 힙에서 가장 작은 데이터를 갖는 노드는 뿌리 노드
힙 순서 속성(Heap Order Property)
- 트리 내의 모든 노드가 부모 노드보다 커야한다
- 자식 > 부모
6.2.1 힙의 삽입 연산
1)힙의 최고 깊이 가장 우측에 새 노드를 추가. 물론 이때 힙은 완전 이진 트리를 유지하도록 해야 함
2) 삽입한 노드를 부모 노드와 비교. 삽입한 노드가 부모 노드보다 크면 제 위치에 삽입된 것이므로 연산을 종료.
반대로 부모 노드보다 작은경우에는 다음 단계를 진행
3) 삽입한 노드가 부모 노드보다 작으면 부모 노드와 삽입한 노드의 위치를 서로 바꿈. 바꾼 후에는 단계 2를 다시 진행
ex) 7 삽입
- 새 노드 7을 힙의 가장 깊은 곳에 추가
- 이때 완전 이진 트리가 무너지면 안되므로 노드 37의 오른쪽 자식으로 추가
- 추가한 노드를 부모 노드와 비교 ->7은 37보다 작으므로 이 두 노드를 교환

- 7과 37이 교환되어 한단계 위로 올라옴
- 또 다시 부모 노드와 비교 -> 7은 8보다 작으므로 이번에도 교환 수행
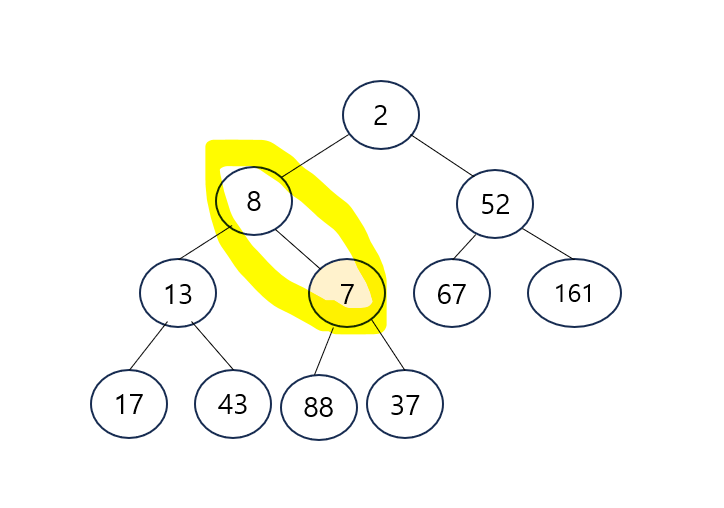
- 7이 또 한 단계 올라옴
- 뿌리 노드 2는 7보다 작으니 힙 순서 속성을 위반하지 않음 -> 삽입 완료

6.2.2 힙의 최솟값 삭제 연산
- 힙의 최솟값 삭제는 곧 뿌리 노드를 삭제한다는 말과 같음
- 뿌리 노드를 삭제한 후 '힙 순서 속성'을 유지하기 위한 뒤처리 과정
1) 힙의 최고 깊이 가장 우측에 있던 노드를 뿌리 노드로 옮겨옴. 이때 힙 순서 속성이 파괴됨
이를 복원하기 위한 작업을 다음 단계부터 시작
2) 옮겨온 노드의 양쪽 자식을 비교하여 작은 쪽 자식과 위치를 교환. (힙 순서 속성을 지키려면 부모 노드는 양쪽 자식보다작은 값을 가져야 하기 때문)
3) 옮겨온 노드가 더 이상 자식이 없는 잎 노드로 되거나 양쪽 자식보다 작은 값을 갖는 경우 삭제 연산 종료
ex)
- 힙에서 최솟값노드(뿌리 노드) 삭제
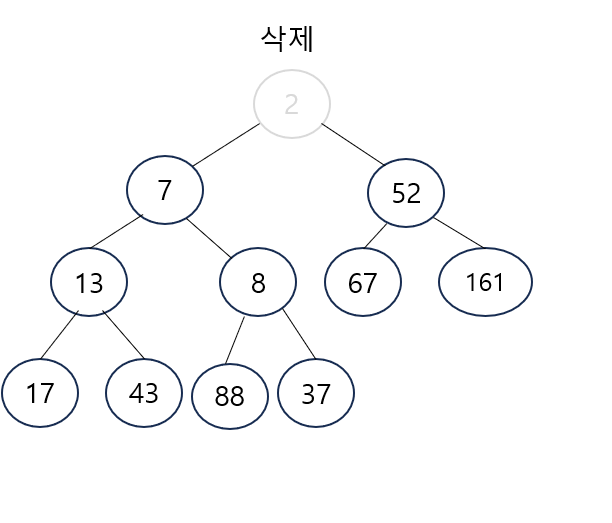
- 힙의 최고 깊이 가장 우측 노드를 삭제된 뿌리 노드가 있던 곳으로 옮김
- 힙 순서 속성에 따르면 부모 노드가 자식 노드보다 작은 값을 가져야 하는데, 뿌리 노드 37이 왼쪽 자식 노드 7보다 크므로 힙 순서 속성 위반
- 뿌리 노드는 양쪽 자식 중 작은 값(7)을 가진 노드와 자신을 교환

- 37이 한 단계 내려옴.
- 37이 양쪽 자식 13과 8보다 큼. 13과 8 중에서 8이 더 작으므로 37 노드와 8노드를 교환
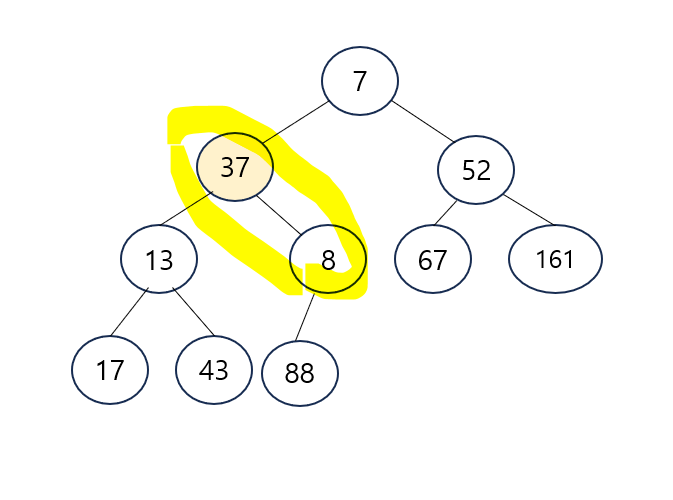
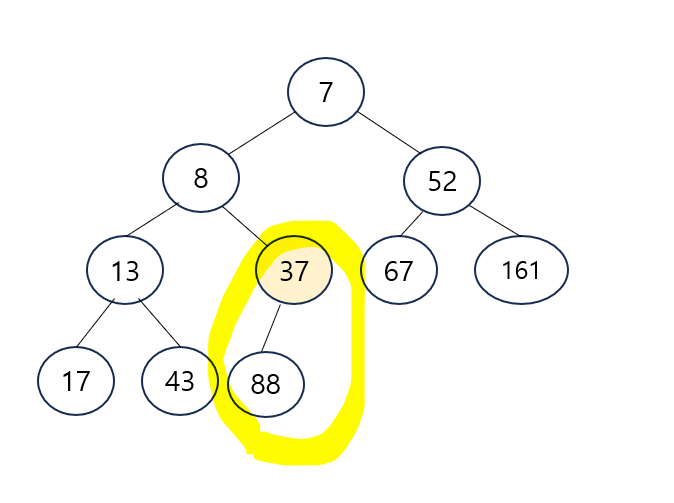
- 37 노드가 한 단계 더 내려옴
- 자식 노드는 88 하나뿐인데 37 노드는 이 보다 더 작으므로 힙 순서 속성을 위반하지 않음
- 삭제 연산 완료
6.2.3 힙의 구현
- 배열을 이용한 힙의 구현
- 배열의 장점은 인덱스 정보만 있으면 힙의 각 노드 위치나 부모와 자식 관계 등을 단번에 알아낼 수 있음
k번 인덱스에 위치한 노드의 양쪽 자식 노드들이 위치한 인덱스
● 왼쪽 자식 노드 : 2k +1
● 오른쪽 자식 노드 : 2k +2
k번 인덱스에 위치한 노드의 부모 노드가 위치한 인덱스 : (k-1)/2
1) 자료구조 선언
- 힙의 각 노드를 표현하는 HeapNode 구조체
- 힙 자체를 표현하는 Heap 구조체
- Capacity 필드는 힙의 용량(Nodes 배열의 크기)
- UsedSize 필드는 실제 배열 안에 들어 있는 큐 요소의 수
typedef int ElementType;
//힙의 노드 구조체
typedef struct tageHeapNode {
ElementType Data;
} HeapNode;
//힙 구조체
typedef struct tagHeap {
HeapNode* Nodes;
int Capacity;
int UsedSize;
} Heap;
2) 삽입 연산 구현
void Heap_Insert(Heap* H, ElementType NewData)
{
int CurrentPosition = H->UsedSize;
//부모 인덱스 반환
int ParentPosition = Heap_GetParent(CurrentPosition);
if(H->UsedSize == H->Capacity)
{
//UsedSize가 Capacity에 도달하면 Capacity를 2배로 늘림
H->Capacity *=2;
H->Nodes = (HeapNode*) realloc(H->Nodes, sizeof(HeapNode) * H->Capacity);
}
H->Nodes[CurrentPosition].Data = NewData;
//후속 처리
while( CurrentPosition >0
&& H->Nodes[CurrentPosition].Data < H->Nodes[ParentPosition].Data )
{
HEAP_SwapNodes(H, CurrentPosition, ParentPosition);
CurrentPostion = ParentPosition;
ParentPosition = HEAP_GetParent(CurrentPosition);
}
H->UsedSize++;
}
3) 최솟값 삭제 연산 구현
- 힙은 항상 최솟값이 뿌리 즉, Nodes 배열의 0번재 요소에 있음
void HEAP_DeleteMin(Heap* H, HeapNode* Root)
{
int ParentPosition = 0;
int LeftPosition = 0;
int RightPosition = 0;
//Root에 최솟값 저장
memcpy(Root, &H->Nodes[0], sizeof(HeapNode));
//배열 0으로 초기화
memset(&H->Nodes[0], 0, sizeof(HeapNode));
H->UsedSize--;
//힙에 첫 번째 요소에 마지막 요소의 값을 복사
HEAP_SwapNodes(H,0,H->UsedSize);
LeftPosition = HEAP_GetLeftChild(0);
RightPosition = LeftPosition + 1;
while(1)
{
int SelectedChild = 0;
if(LeftPosition >= H->UsedSize)
break;
if(RightPosition >= H->UsedSize)
{
SelectedChild = LeftPosition;
}
else {
if(H->Nodes[LeftPosition].Data > H->Nodes[RightPosition].Data)
SelectedChild = RightPosition;
else
SelectedChild = LeftPosition;
}
if(H->Nodes[SelectedChild].Data < H->Nodes[ParentPosition].Data)
{
HEAP_SwapNodes(H, ParentPosition, SelectedChild);
ParentPosition = SelectedChild;
}
else
break;
LeftPosition = HEAP_GetLeftChild(ParentPosition);
RightPosition = LeftPosition + 1;
}
if(H->UsedSizs < (H->Capacity / 2))
{
H-<Capacity /=2;
H->Nodes =
(HeapNode*)realloc(H->Nodes, sizeof( HeapNode) * H->Capacity);
}
}
6.3 힙 기반 우선순위 큐의 구현
- 힙은 최솟값(최댓값)을 즉시 얻어낼 수 있게 한다는 점에서 우선순위 큐를 구현하는데 적격인 자료구조
#include <stdio.h>
#include <memory.h>
#include <stdlib.h>
typedef int PriorityType;
typedef struct tagePQNode
{
PriorityType Priority;
void* Data;
}PQNode;
typedef struct tagPriorityQueue
{
PQNode* Nodes;
int Capacitiy;
int UsedSize;
}PriorityQueue;
//우선순위 큐 생성
PriorityQueue* PQ_Create(int IntitialSize)
{
PriorityQueue* NewPQ = (PriorityQueue*)malloc(sizeof(PriorityQueue));
NewPQ->Capacitiy = IntitialSize;
NewPQ->UsedSize = 0;
NewPQ->Nodes = (PQNode*)malloc(sizeof(PQNode) * NewPQ->Capacitiy);
return NewPQ;
}
//우선순위 큐 제거
void PQ_Destroy(PriorityQueue* PQ)
{
free(PQ->Nodes);
free(PQ);
}
//우선순위 큐 노드 삽입
void PQ_Enqueue(PriorityQueue* PQ, PQNode NewNode)
{
int CurrentPosition = PQ->UsedSize;
int ParentPosition = PQ_GetParent(CurrentPosition);
if (PQ->UsedSize == PQ->Capacitiy)
{
if (PQ->Capacitiy == 0)
PQ->Capacitiy = 1;
PQ->Capacitiy *= 2;
PQ->Nodes = (PQNode*)realloc(PQ->Nodes, sizeof(PQNode) * PQ->Capacitiy);
}
PQ->Nodes[CurrentPosition] = NewNode;
//후속처리
while (CurrentPosition > 0
&& PQ->Nodes[CurrentPosition].Priority
< PQ->Nodes[ParentPosition].Priority)
{
PQ_SwapNodes(PQ, CurrentPosition, ParentPosition);
CurrentPosition = ParentPosition;
ParentPosition - PQ_GetParent(CurrentPosition);
}
PQ->UsedSize++;
}
// 노드 교체
void PQ_SwapNodes(PriorityQueue* PQ, int Index1, int Index2)
{
int CopySize = sizeof(PQNode);
PQNode* Temp = (PQNode*)malloc(CopySize);
memcpy(Temp, &PQ->Nodes[Index1], CopySize);
memcpy(&PQ->Nodes[Index1], &PQ->Nodes[Index1], CopySize);
memcpy(&PQ->Nodes[Index2],Temp, CopySize);
free(Temp);
}
//우선순위 큐 노드 삭제
void PQ_Dequeue(PriorityQueue* PQ, PQNode* Root)
{
int ParentPosition = 0;
int LeftPosition = 0;
int RightPosition = 0;
memcpy(Root, &PQ->Nodes[0], sizeof(PQNode));
memset(&PQ->Nodes[0], 0, sizeof(PQNode));
PQ->UsedSize--;
PQ_SwapNodes(PQ, 0, PQ->UsedSize);
LeftPosition = PQ_GetLeftChild(0);
RightPosition = LeftPosition + 1;
while (1)
{
int SelectedChild = 0;
if (LeftPosition >= PQ->UsedSize)
break;
if (RightPosition >= PQ->UsedSize)
{
SelectedChild = LeftPosition;
}
else {
if (PQ->Nodes[LeftPosition].Priority
> PQ->Nodes[RightPosition].Priority)
SelectedChild = RightPosition;
else
SelectedChild = LeftPosition;
}
if (PQ->Nodes[SelectedChild].Priority
< PQ->Nodes[ParentPosition].Priority)
{
PQ_SwapNodes(PQ, ParentPosition, SelectedChild);
ParentPosition = SelectedChild;
}
else
break;
LeftPosition = PQ_GetLeftChild(ParentPosition);
RightPosition = LeftPosition + 1;
}
if (PQ->UsedSize < (PQ->Capacitiy / 2))
{
PQ->Capacitiy /= 2;
PQ->Nodes =
(PQNode*)realloc(PQ->Nodes, sizeof(PQNode) * PQ->Capacitiy);
}
}
//부모 인덱스 반환
int PQ_GetParent(int index)
{
return (int)((index - 1) / 2);
}
//왼쪽 자식 인덱스 반환
int PQ_GetLeftChild(int index)
{
return (2 * index) + 1;
}
//큐 비어있는지
int PQ_IsEmpty(PriorityQueue* PQ)
{
return (PQ->UsedSize == 0);
}
// 노드 출력
void PrintNode(PQNode* Node)
{
printf("작업명: %s (우선순위:%d)\n", Node->Data, Node->Priority);
}
int main(void)
{
PriorityQueue* PQ = PQ_Create(3);
PQNode Popped;
PQNode Nodes[7] =
{
{34, (void*)"코딩"},
{12, (void*)"고객미팅"},
{87, (void*)"커피타기"},
{45, (void*)"문서작성"},
{35, (void*)"디버깅"},
{66, (void*)"이닦기"}
};
PQ_Enqueue(PQ, Nodes[0]);
PQ_Enqueue(PQ, Nodes[1]);
PQ_Enqueue(PQ, Nodes[2]);
PQ_Enqueue(PQ, Nodes[3]);
PQ_Enqueue(PQ, Nodes[4]);
PQ_Enqueue(PQ, Nodes[5]);
printf("큐에 남아 있는 작업의 수:%d\n", PQ->UsedSize);
while (!PQ_IsEmpty(PQ))
{
PQ_Dequeue(PQ, &Popped);
PrintNode(&Popped);
}
return 0;
}
'C언어 > 알고리즘' 카테고리의 다른 글
| [알고리즘] ch 7. 그래프 (2) - 위상 정렬 (0) | 2023.10.25 |
|---|---|
| [알고리즘] ch 7. 그래프 (1) (0) | 2023.10.25 |
| [알고리즘] ch 5. 탐색(3) - 레드 블랙 트리 (2) | 2023.10.11 |
| [알고리즘] ch 5. 탐색(2) - 이진 탐색 트리 (0) | 2023.09.22 |
| [알고리즘] ch 5. 탐색 (1)- 순차 탐색, 이진 탐색 (0) | 2023.09.21 |



