1. 통계적으로 추론하기
1) 모수 검정이란
- 통계학에서는 모집단(population)에 대한 파라미터를 추정하는 방법을 모수검정(parametric test)이라고 한다.
- 파라미터는 평균, 분산 등이며 모집단은 관심 대상이 되는 전체 데이터를 의미한다.
- 모집단에서 선택한 일부 샘플은 표본(sample)이라고 부른다.
2) 표준점수 구하기
- 데이터가 정규분포를 따른다고 가정하고, 각 값이 평균에서 얼마나 떨어져 있는지 표준편차를 사용해 변환한 점수를 표준 점수(standard score) 또는 z 점수(z score)이라고 한다.
- z 점수는 평균까지 거리를 표준편차로 나눈 것이다.

z 점수 구하기
- 다섯 개의 값으로 이루어진 배열 x가 있을 때 숫자 7에 대한 z 점수를 계산하려면, 넘파이로 먼저 표준편차와 평균을 계산한 후 z 점수 공식에 적용할 수 있다.
import numpy as np
x=[0,3,5,7,10]
s = np.std(x) #표준편차를 구한다.
m = np.mean(x) #평균을 구한다.
z = (7-m)/s
print(z)

- z 점수는 사이파이(scipy)로 더 편리하게 계산할 수 있따.
- 사이파이의 stats 모듈을 임포트한 다음 zscore() 함수를 호출하여 배열 x에 대한 모든 z 점수를 계산할 수 있다.
from scipy import stats
stats.zscore(x)
누적분포 이해하기
- 평균이 0이고 표준편차가 1인 정규분포를 표준정규분포라고 한다. 평균이 0이고 표준편차가 1을 z 점수 공식에 대입하면 z = x가 된다. 따라서 표준정규분포는 z 점수를 사용해 전체 데이터가 어떻게 분포되어 있는지 나타낼 수 있다.
ex)
- 표준정규분포에서 z 점수가 1.0 이내에 위치한 샘플은 전체의 약 68%에 해당한다. z 점수 2.0 이내에 위치한 샘플은 전체의 약 95%에 해당한다.

누적분포 구하기
- 어떤 z 점수 이내의 샘플 비율을 편리하게 계산할 수 있는 함수가 사이파이에 있다.
- stats 모듈의 norm.cdf() 메서드는 누적된 분포를 반환해준다.
- norm.cdf() 메서드에 평균 0을 전달하여 0까지의 비율을 구한다.
- 50%를 의미하는 0.5가 출력되었다.
stats.norm.cdf(0)

- 만약 z 점수 1 이내의 비율을 구하려면 z 점수 1까지 누적분포에서 z 점수 -1까지 누적분포를 빼면 된다.
stats.norm.cdf(1.0) - stats.norm.cdf(-1.0)


- 표준편차 2 이내의 비율
stats.norm.cdf(2.0) - stats.norm.cdf(-2.0)
- 전체에서 특정 비율에 해당하는 z 점수를 구하려면 norm.ppf() 메서드를 사용한다.
ex) 90% 누적분포에 해당하는 z 점수
stats.norm.ppf(0.9)
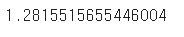
3) 중심극한정리 알아보기
- 중심극한정리(central limit theorem)는 '무작위로 샘플을 뽑아 만든 표본의 평균은 정규분포에 가깝다'는 이론이다.
- 왼쪽에 모집단이 있을 때 여기서 30개의 샘플을 뽑아 표본을 만든다. 그다음 표본의 평균을 계산한다. 이런 과정을 여러 번 반복해서 1,000개의 평균을 만들어 놓는다. 그리고 이 1,000개의 평균을 히스토그램을 그리면 정규분포를 따른다.

- 남산도서관 대출 데이터를 사용
import pandas as pd
ns_book7 = pd.read_csv('ns_book7.csv', low_memory=False)
ns_book7.head()

- ns_book7 데이터프레임의 '대출건수' 열로 히스토그램을 그린다.
import matplotlib.pyplot as plt
plt.hist(ns_book7['대출건수'], bins=50)
plt.yscale('log')
plt.show()

샘플링하기
- 무작위로 1,000개의 표본을 샘플링하여 각 평균을 리스트로 저장
- 무작위 샘플링을 위해 판다스 데이터프레임의 sample() 메서드를 사용
- 이 메서드의 첫 번째 매개변수에는 샘플링할 개수를 지정한다. 그 다음 mean() 메서드를 연이어 호출하여 샘플링 결과의 평균을 계산한다. 마지막으로 이 평균을 sample_means 리스트에 추가한다. 이 과정을 for문으로 1,000번을 반복한다.
np.random.seed(42)
sample_means = []
for _ in range(1000):
m = ns_book7['대출건수'].sample(30).mean()
sample_means.append(m)
plt.hist(sample_means, bins=30)
plt.show()

샘플링 크기와 정확도
- 이 정규분포 형태의 평균이 모집단의 평균과 매우 가깝다
- sample.means 배열의 평균을 확인
np.mean(sample_means) ## 무작위로 뽑은 표본의 통계량

- ns_book7 데이터프레임에 있는 전체 대출건수의 평균 확인
ns_book7['대출건수'].mean() ##실제 모집단의 통계량

- 일반적으로 중심극한정리를 따르려면 샘플링의 크기가 30보다 클수록 좋다.
- 샘플링 크기를 20으로 낮추어 평균을 계산
np.random.seed(42)
sample_means = []
for _ in range(1000):
m = ns_book7['대출건수'].sample(20).mean()
sample_means.append(m)
np.mean(sample_means)
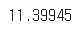
- 표본의 평균이 대출건수 실제 평균에서 더 멀어졌다.
- 샘플링 크기를 40으로 높여서 다시 평균 구하기
np.random.seed(42)
sample_means = []
for _ in range(1000):
m = ns_book7['대출건수'].sample(40).mean()
sample_means.append(m)
np.mean(sample_means)

- 샘플링 크기를 늘리니 대출건수 평균 11.59에 더욱 가까워졌다.
- 또 다른 특징은 표본 평균의 표준편차가 모딥단의 표준 편차를 표본 크기의 제곱근으로 나눈 것에 가깝다는 것이다.

- 실제로 이 공식이 잘 들어 맞는지 확인. 먼저 넘파이 std() 함수로 sample_means의 표준편차를 구한다.
np.std(sample_means)

- 전체 대출건수의 표준편차를 샘플링 개수 40의 제곱근으로 나누어 본다.
np.std(ns_book7['대출건수']) / np.sqrt(40)
- 이렇게 구한 표본 평균의 표준편차는 표준오차(standard error)라고 한다.
4) 모집단의 평균 범위 측정하기 : 신뢰구간
- 신뢰구간(confidence interval)은 표본의 파라미터가 속할 것이라 믿는 모집단의 파라미터 범위이다.
- 남산도서관의 파이썬 도서의 대출건수를 사용해 신뢰구간을 어떻게 계산하는지 알아보기
- 주제분류번호가 '00'으로 시작하고 도서명에 '파이썬'이 포함된 행을 불리언 배열로 인덱스 python_books_index를 만들어 도서를 추출한다.
python_books_index = ns_book7['주제분류번호'].str.startswith('00') & \
ns_book7['도서명'].str.contains('파이썬')
python_books = ns_book7[python_books_index]
python_books.head()

- len() 함수를 사용해 도서가 모두 몇 권인지 확인
len(python_books)

- 파이썬 도서의 대출건수 평균을 계산
python_mean = np.mean(python_books['대출건수'])
python_mean

- z 점수 공식과 중심극한정리를 연결하여 모집단의 평균 범위를 예측
- 모집단의 평균을 알 수 없고, 표본의 평균만 알 때 표본의 평균에 대한 z 점수 공식은 다음처럼 쓸 수 있다.

- 모집단의 평균 u를 남기고 다른 항을 정리하면 표본의 평균에서 z 점수와 표준오차를 곱한 값을 빼는 식이 완성된다.

- 남산도서관의 파이썬 대출건수가 표본이라면 우리나라 모든 도서관의 파이썬 도서 대출건수를 모집단으로 생각할 수 있다. 이럴 때 중심극한정리를 적용해 볼 수 있다. 모집단의 표준편차가 표본의 표준편차와 비슷하다고 가정하는 것이다.
- 따라서 모집단의 표준편차 대신 표본이라 할 수 있는 남산도서관의 파이썬 도서 대출건수로 표준편차를 구한ㄷ 다음, 표준 오차를 계산
python_std = np.std(python_books['대출건수'])
python_se = python_std / np.sqrt(len(python_books))
python_se

- 마지막으로 표준오차에 곱할 적절한 z 점수를 결정해야 한다. 여기에서는 이 표본의 평균이 모집단의 평균을 중심으로 95% 이내 구간에 포함된다고 확신하고 싶다.
- 평균을 중심으로 95% 영역을 차지하면 좌우에는 각각 2.5%가 남는다. 따라서 95% 비율에 해당하는 z 점수를 알려면 norm.ppf() 메서드에 각각 0.975와 0.025를 입력하면 된다.
stats.norm.ppf(0.975)
stats.norm.ppf(0.025)

- 정규분포는 대칭이기 때문에 이 두 z점수가 부호만 다르고 같은 것을 알 수 있다.
- 표준오차 python_se와 z 점수를 곱하여 파이썬 도서의 대출건수 평균 python_mean 데이터프레임이 속할 범위를 구해본다.
print(python_mean-1.96*python_se, python_mean+1.96*python_se)

- 표본의 평균 python_mean과 표준 오차 python_se를 바탕으로 '모집단의 평균이 13.2에서 16.3 사이에 놓여 있을 거라 95% 확신한다'고 말한다. 또는 '95% 신뢰구간에서 파이썬 도서의 모집단 평균이 13.2에서 16.3 사이에 놓여 있다'고 말한다.
5) 통계적 의미 확인하기 : 가설검정
- 가설검정은 표본에 대한 정보를 사용해 모집단의 파라미터에 대한 가정을 검정하는 것이다.
- 예를들어 파이썬과 C++ 도서의 평균 대출건수가 같다고 가정했을 때, 파이썬과 C++ 도서의 표본을 각각 추출하여 이 가정이 맞는지 검정할 수 있다.
영가설(null hypothesis)
- 귀무가설
- 표본 사이에 통계적 의미가 없다고 예상되는 사실
- 파이썬과 C++ 도서의 평균 대출건수가 같다는 가설
대립가설(alternative hypothesis)
- 표본 사이에 통계적인 차이가 있다는 가설
- 파이썬과 C++ 도서의 평균 대출건수가 같지 않다는 가설
- 두 모집단의 평균에 대한 z 점수 공식
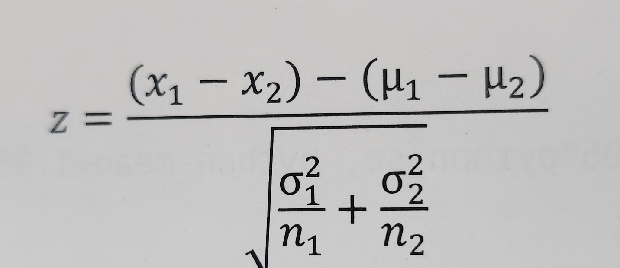
- 영가설의 경우 두 모집단의 평균에 차이가 없을 것이라 가정한다. 따라서 u1-u2=0으로 놓고 z점수를 계산할 수 있다. 이렇게 계산한 z 점수가 일정 수준 이하라면 영가설이 맞는다고 했을 때, 평균에 차이가 없는 데이터가 관측될 가능성이 매우 낮다는 의미이다. 따라서 영가설을 기각하고 두 모집단의 평균에 차이가 있다는 대립가설을 채택할 수 있다.
- z 점수에 대한 이런 기준을 유의수준(significance level)이라고 한다.
z 점수로 가설 검증하기
- C++ 도서에 대한 불리언 배열의 인덱스를 만들어 cplus_books 데이터프레임을 만든다.
cplus_books_index = ns_book7['주제분류번호'].str.startswith('00') & \
ns_book7['도서명'].str.contains('C++', regex=False)
cplus_books = ns_book7[cplus_books_index]
cplus_books.head()

- C++ 도서권수
len(cplus_books)

- C++ 도서의 평균 대출건수
cplus_mean = np.mean(cplus_books['대출건수'])
cplus_mean

- z 점수에 대한 가설 검정 공식으로 확인
- C++ 도서에 대한 표준오차 계산
cplus_se = np.std(cplus_books['대출건수'])/ np.sqrt(len(cplus_books))
cplus_se

(python_mean - cplus_mean) / np.sqrt(python_se**2 + cplus_se**2)

- 계산된 z 점수를 사용해 누적분포를 확인
stats.norm.cdf(2.50)

- 2.50에 해당하는 누적분포는 0.994이다. 따라서 정규분포의 양쪽 끝의 면적은 각각 1-0.994 = 0.006이 된다.
- p-값은 (1-0.994)*2=0.01로 유의수준에 해당하는 0.05(5%)보다 작다. 따라서 영가설을 기각하며 '파이썬과 C++ 도서의 평균에 차이가 있다'는 대립가설이 지지된다.
t-검정으로 가설 검증하기
- 사이파이에 두 표본의 평균을 비교하는 ttest_ind() 함수가 있다. ttest_ind() 함수는 t-분포인 두 표본을 비교하는 t-검정을 수행한다.
- t-분포(t-distribution)은 정규분포와 비슷하지만, 중앙은 조금 더 낮고 꼬리가 더 두꺼운 분포이다.
- 표본의 크기가 30 이하일 때 t-분포를 사용하는 것이 좋으며 표본 크기가 30보다 크면 t-분포는 정규분포와 매우 비슷해진다.
- 파이썬 도서와 C++ 도서의 데이터를 ttest_ind() 함수에 전달하면 t 점수와 p-값을 반환한다.
t, pvalue = stats.ttest_ind(python_books['대출건수'], cplus_books['대출건수'])
print(t, pvalue)

- p-값은 0.03으로 영가설의 기각 기준은 0.05보다 작다. 따라서 영가설을 기각하며 두 도서의 대출건수 평균의 차이는 우연이 아니라고 말할수 있다.
6) 정규분포가 아닐 때 검증하기 : 순열 검정
- 순열검정(permutation test)은 모집단의 분포가 정규분포를 따르지 않거나 모집단의 분포를 알 수 없을 때 사용할 수 있는 방법이다.
- 모집단의 파라미터를 추정하지 않기 때문에 비모수검정(nonparametric test) 방법 중 하나이다.
- 먼저 두 표본의 평균의 차이를 계산한 후 도 표본을 섞고 무작위로 두 그룹을 나눈다. 이때 두 그룹은 원래 표본의 크기와 동일하게 만든다. 이렇게 나눈 두 그룹에서 다시 평균의 차이를 계산한다. 이런 과정을 여러 번 반복해서 원래 표본의 평균 차이가 무작위로 나눈 그룹의 평균 차이보다 크거나 작은 경우를 헤아려 p-값을 계산한다.
도서 대출건수 평균비교하기(1) : 파이썬 vs C++
- 두 개의 배열을 받아 평균을 구하는 statistic() 함수를 만든다.
def statistic(x, y):
return np.mean(x) - np.mean(y)
- 두 배열을 넘파이 append() 함수로 합친 후 무작위로 추출하기 위해 permutation() 함수를 사용한다. 이 함수는 무작위로 섞인 배열을 만드는데, 여기에서는 전체 배열 길이만큼 랜덤한 인덱스를 만들어 준다. 인덱스로 x_,y_ 두 그룹을 나눈 후 그룹사이의 평균 차이를 계산한다. 이런 식으로 모두 1,000번의 순열 검정을 수행한다.
def permutation_test(x, y):
# 표본의 평균 차이를 계산합니다.
obs_diff = statistic(x, y)
# 두 표본을 합칩니다.
all = np.append(x, y)
diffs = []
np.random.seed(42)
# 순열 검정을 1000번 반복합니다.
for _ in range(1000):
# 전체 인덱스를 섞습니다.
idx = np.random.permutation(len(all))
# 랜덤하게 두 그룹으로 나눈 다음 평균 차이를 계산합니다.
x_ = all[idx[:len(x)]]
y_ = all[idx[len(x):]]
diffs.append(statistic(x_, y_))
# 원본 표본보다 작거나 큰 경우의 p-값을 계산합니다.
less_pvalue = np.sum(diffs < obs_diff)/1000
greater_pvalue = np.sum(diffs > obs_diff)/1000
# 둘 중 작은 p-값을 선택해 2를 곱하여 최종 p-값을 반환합니다.
return obs_diff, np.minimum(less_pvalue, greater_pvalue) * 2
- 표본의 평균 차이보다 큰 경우와 작은 경우의 비율을 계산하여 p-값을 계산한다.
- 일반적으로 영가설을 기각하는 것이 목적이므로 둘 중에 작은 값을 선택하고 2를 곱해 양쪽 꼬리에 해당하는 비율을 얻는다.
- 이 값이 바로 '영가설이 옳다고 가정했을 때 이런 데이터가 관측될 확률'이다.
permutation_test(python_books['대출건수'], cplus_books['대출건수'])
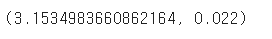
- 여기에서도 p-값이 5%에 해당하는 유의수준에 미치지 못하기 때문에 영가설을 기각하고 두 도서의 평균 대출건수에는 차이가 있다고 결론 내릴 수 있다.
도서 대출건수 평균 비교하기(2) : 파이썬 vs 자바스크립트
- 도서 제목에 '자바스크립트' 키워드가 들어간 행 추출
java_books_indx = ns_book7['주제분류번호'].str.startswith('00') & \
ns_book7['도서명'].str.contains('자바스크립트')
java_books = ns_book7[java_books_indx]
java_books.head()

- 자바스크립트의 도서권수와 평균 대출 건수 확인
print(len(java_books), np.mean(java_books['대출건수']))

- 순열 검정 확인
permutation_test(python_books['대출건수'], java_books['대출건수'])

- p-값이 0.05보다 훨씬 크다. 따라서 영가설을 기각할 수 없으며 파이썬과 자바스크립트 도서 사이의 평균 대출건수 차이는 큰 의미가 없다고 볼 수 있다.
2. 머신러닝으로 예측하기
1) 모델 훈련하기
- 입력 A, 타깃 A를 훈련 세트(training set)이라 부르고 입력 B, 타깃 B를 테스트 세트(test set)라고 부른다.
- 보통 테스트 데이터는 전체 데이터의 20~25% 정도 사용한다.
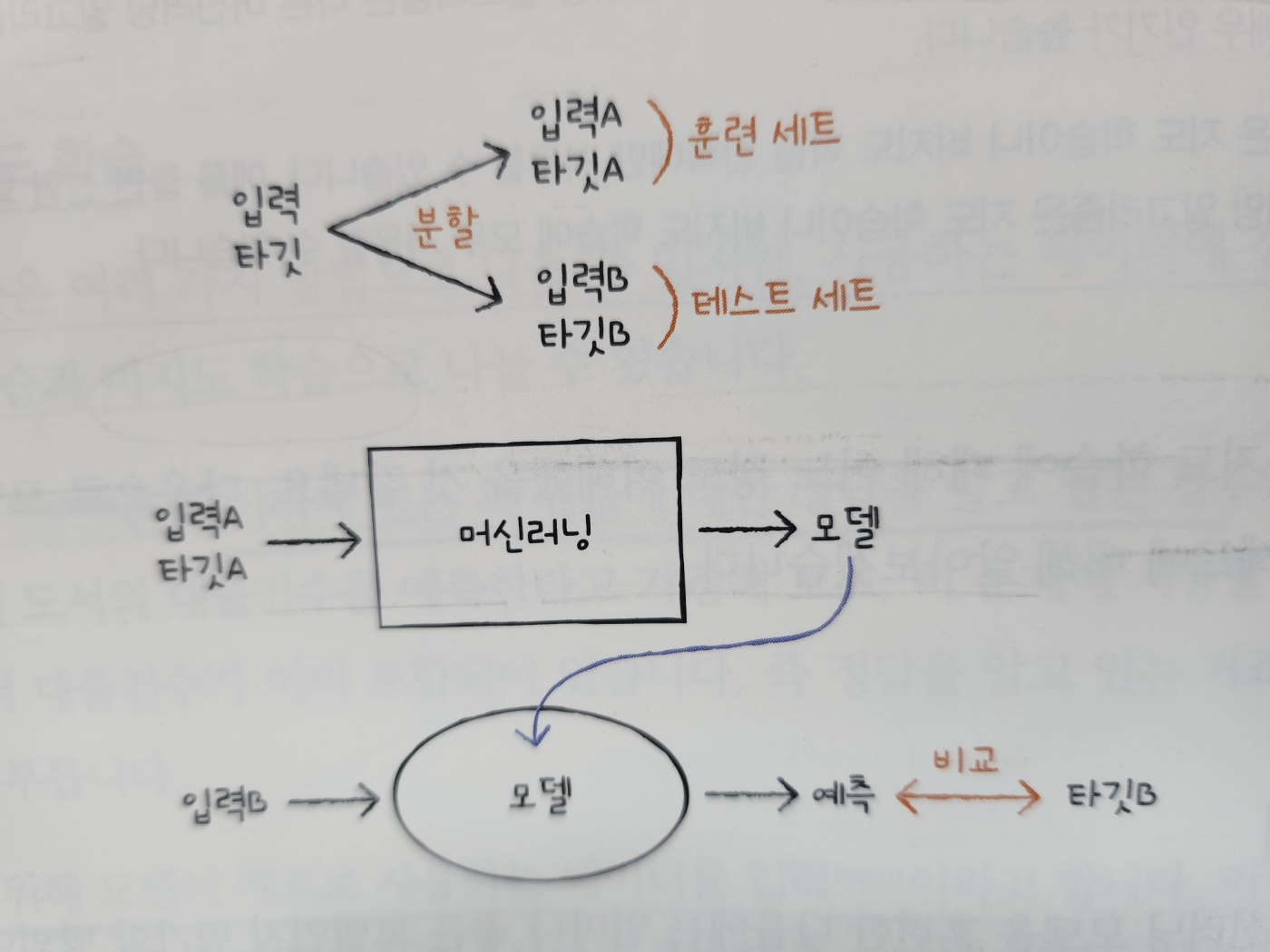
훈련 세트와 테스트 세트로 나누기
- 데이터를 무작위로 섞은 후 훈련 세트와 테스트 세트로 나눈다.
- train_test_split() 함수는 기본적으로 입력된 데이터를 무작위로 섞은 후 75%를 훈련 세트로 25%를 테스트 세트로 나눈다. 이 함수는 분할된 훈련 세트와 테스트 세트를 리스트로 반환하기 때문에 리스트 개수에 맞는 변수를 왼쪽에 나열하여 반환되는 값을 저장할 수 있다.
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(ns_book7, random_state=42)
print(len(train_set), len(test_set))
- 사이킷런에 있는 선형 회귀 모델을 이 데이터로 훈련
- train_set에 있는 '도서권수'열을 사용해 대출건수를 예측
- train_set에서 '도서권수'열과 '대출건수'열을 각각 X_train와 y_train 변수에 저장하고 크기 확인
X_train = train_set[['도서권수']]
y_train = train_set['대출건수']
print(X_train.shape, y_train.shape)

- 열 하나를 선택할 때 리스트로 감싸면 X_train이 282,577개의 행과 1개의 열로 이루어진 데이터프레임이 된다. 이를 2차원 배열처럼 생각할 수 있다.
- 반면 y_train은 시리즈 객체, 즉 282,577개의 원소를 가진 1차원 배열이다.
- 이렇게 데이터를 준비한 이유는 사이킷런이 입력으로는 2차원 배열, 타깃으로는 1차원 배열을 기대하기 때문이다.
- 2차원 배열인 입력은 행 방향으로 샘플이 나열되고 열 방향으로 샘플의 속성이 나열된다. 머신러닝에서 이런 속성을 특성(feature)라고도 부른다.
선형 회귀 모델 훈련하기
- 사이킷런의 linear_model 모듈 아래에 있는 LinearRegression 클래스를 임포트해서 선형 회귀 모델을 훈련
- 선형 회귀 알고리즘인 LinearRegression 클래스의 객체 lr을 만들고 이 객체의 fit() 메서드를 호출하여 모델을 훈련할 수 있다.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train, y_train)
2) 훈련된 모델을 평가하기 : 결정계수
- 사이킷런의 머신러닝 모델은 모두 score() 메서드를 제공한다. 이 메서드를 사용해 훈련된 머신러닝 모델이 얼마나 유용한지를 평가할 수 있다.
X_test = test_set[['도서권수']]
y_test = test_set['대출건수']
lr.score(X_test, y_test)
- score() 메서드가 반환하는 이 점수는 보통 0~1 사이의 값을 가진다. 이러한 점수를 결정계수(coefficeient of determination)이라고 부른다.

- 평균은 타깃의 평균을 의미한다. 예측이 평균에 가까워지면 분모와 분자가 같아져 R^2 점수는 0이 된다.
- 만약 타깃에 정확히 맞는 예측을 하면 분자가 0에 가까워지고 R^2 점수는 1이 된다.
- 결정계수가 1에 가까울수록 도서권수와 대출건수간에 관계가 깊다고 볼 수 있다.
3) 연속적인 값 예측하기 : 선형회귀
- 선형 회귀(linear regression)은 선형 함수(linear function)를 사용해 모델을 만드는 알고리즘이다.
y=a*x+b
- x는 입력이고 y는 타깃이다. 입력에 기울기 a를 곱하고 y축고 만나는 절편 b를 더하여 예측을 만드는 것이 바로 선형 회귀 알고리즘이다.
- 선형 회귀 알고리즘이 fit() 메서드를 호출했을 때 데이터에서 학습한 것이 바로 이 기울기 a와 절편 b이다.
- lr 객체의 coef_ 속성과 intercept_ 속성에 학습된 기울기와 절편이 각각 저장되어 있다.
print(lr.coef_, lr.intercept_)

4) 카테고리 예측하기 : 로지스틱 회귀
- 지도 학습 중에서 타깃이 실수인 문제를 회귀라고 한다. 대표적인 회귀 알고리즘이 선형 회귀이다. 하지만 타깃이 실수가 아니라 어떤 종류의 카테고리(범주)인 경우도 있다.
- 두 개의 카테고리로 구분하는 경우는 이진 분류(binaray classification), 세 개 이상의 카테고리로 구분하는 경우를 다중 분류(multiclass classification)이라고 한다.
- 분류 알고리즘에서는 타깃 카테고리를 클래스(class)라고 부른다. 일반적으로 이진 분류의 타깃은 0 또는 1이다. 0일 때는 음성 클래스 (negative class), 1인 경우를 양성 클래스(positive class)라고 부른다.
- 분류 알고리즘 중에 대표적인 알고리즘은 로지스틱 회귀(logistic regression)이다. 선형회귀처럼 선형 함수를 사용하지만, 예측을 만들기 전에 로지스틱 함수(logistic function)를 거치는 과정이 있다. 로지스틱 함수를 사용해 연속적인 실수 출력값을 1 또는 0으로 변환한다.
-> 선형 함수의 결괏값 실수 z를 로지스틱 함수에 통과시키면 y는 0~1사이의 값이 된다. 이때 y는 0.5보다 크면 양성 클래스로 예측하고, 0.5보다 작으면 음성 클래스로 예측한다.
로지스틱 회귀 모델 훈련하기
- 모델을 만들기 전 먼저 타깃 y_train과 y_test를 이진 분류에 맞게 바꾸어야 한다.
- 즉, 음성 클래스에 해당하는 0과 양성 클래스에 해당하는 1로 바꾸어야 한다.
- 전체 대출건수 평균보다 높으면 양성 클래스로 그렇지 않으면 음성 클래스로 만든다.
borrow_mean = ns_book7['대출건수'].mean()
y_train_c = y_train > borrow_mean
y_test_c = y_test > borrow_mean
- 사이킷런의 linear_model 모듈에 있는 LogisticRegression 클래스를 임포트하여 선형 회귀 모델을 훈련했을 떄와 마찬가지로 훈련 세트로 fit() 메서드를 호출한다.
from sklearn.linear_model import LogisticRegression
logr = LogisticRegression()
logr.fit(X_train, y_train_c)
logr.score(X_test, y_test_c)

- 사이킷런의 분류 모델의 경우 score() 메서드가 출력하는 함수는 정확도(accuracy)이다. 정확도란 입력 데이터 중 정답을 맞춘 비율이다.
양성 클래스와 음성 클래스 분포 확인하기
- 시리즈 객체인 y_test_c에서 value_counts() 메서드를 호출해 값의 분포 알아보기
y_test_c.value_counts() #시리즈의 고유한 값의 개수를 세어 반환

- 음성 클래스가 69% 정도이고 양성 클래스는 31%이다. 이런 불균형한 데이터에서는 71%의 정확도가 그다지 높은 편은 아니다.
- 사이킷런은 가장 많은 클래스로 무조건 예측을 수행하는 더미(dummy) 모델을 제공한다. 회귀일 경우 DummyRegressor 모델이 있으며 무조건 타깃의 평균을 예측한다. 분류일 경우 DummyClassifier 모델이 기본적으로 가장 많은 클래스를 예측으로 출력한다.
- DummyClassifier()를 사용해 score() 메서드의 결과 확인
from sklearn.dummy import DummyClassifier
dc = DummyClassifier()
dc.fit(X_train, y_train_c)
dc.score(X_test, y_test_c)

- 예상대로 69%의 정확도가 출력되었다. 이 값이 모델을 만들 때 기준점이 된다. 적어도 이 점수보다 낫지 않다면 유용한 모델이라고 말하기 어렵다.
'데이터 > 데이터 분석' 카테고리의 다른 글
| [혼공] ch 6. 복잡한 데이터 표현하기 (0) | 2024.07.09 |
|---|---|
| [혼공] ch 5. 데이터 시각화하기 (0) | 2024.07.09 |
| [혼공] ch 4. 데이터 요약하기 (1) | 2024.07.05 |
| [혼공] ch 3. 데이터 정제하기 (0) | 2024.07.04 |
| [혼공] ch 2. 데이터 수집하기 (0) | 2024.07.03 |



